
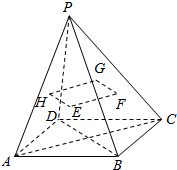
 如图所示,已知四边形ABCD是平行四边形,P点是四边形ABCD所在平面外一点,连接PA、PB、PC、PD,设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.试用向量法证明E、F、G、H四点共面.
如图所示,已知四边形ABCD是平行四边形,P点是四边形ABCD所在平面外一点,连接PA、PB、PC、PD,设点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心.试用向量法证明E、F、G、H四点共面. 分析 画出图形,利用三角形的重心定义,结合平面向量的线性运算法则,得出$\overrightarrow{EG}$=$\overrightarrow{EF}$+$\overrightarrow{EH}$,
即证E、F、G、H四点共面.
解答 证明:分别延长PE、PF、PG、PH,交对边于M、N、Q、R点,
因为E、F、G、H分别是所在三角形的重心,
所以M、N、Q、R为所在边的中点,
顺次连接M、N、Q、R得到的四边形为平行四边形,
且有$\overrightarrow{PE}$=$\frac{2}{3}$$\overrightarrow{PM}$,$\overrightarrow{PF}$=$\frac{2}{3}$$\overrightarrow{PN}$,$\overrightarrow{PG}$=$\frac{2}{3}$$\overrightarrow{PQ}$,$\overrightarrow{PH}$=$\frac{2}{3}$$\overrightarrow{PR}$;如图所示,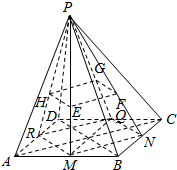
∴$\overrightarrow{MQ}$=$\overrightarrow{MN}$+$\overrightarrow{MR}$=($\overrightarrow{PN}$-$\overrightarrow{PM}$)+($\overrightarrow{PR}$-$\overrightarrow{PM}$)
=$\frac{3}{2}$($\overrightarrow{PF}$-$\overrightarrow{PE}$)+$\frac{3}{2}$($\overrightarrow{PH}$-$\overrightarrow{PE}$)
=$\frac{3}{2}$($\overrightarrow{EF}$+$\overrightarrow{EH}$);
又∵$\overrightarrow{MQ}$=$\overrightarrow{PQ}$-$\overrightarrow{PM}$=$\frac{3}{2}$$\overrightarrow{PG}$-$\frac{3}{2}$$\overrightarrow{PE}$=$\frac{3}{2}$$\overrightarrow{EG}$,
∴$\frac{3}{2}$$\overrightarrow{EG}$=$\frac{3}{2}$($\overrightarrow{EF}$+$\overrightarrow{EH}$),
∴$\overrightarrow{EG}$=$\overrightarrow{EF}$+$\overrightarrow{EH}$
由共面向量定理知:E、F、G、H四点共面.
点评 本题考查了平面向量线性运算与应用问题,也考查了空间想象与逻辑推理能力,是中档题目.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北石家庄一中高一下期末数学(文)试卷(解析版) 题型:解答题
数列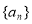 的前
的前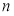 项和记为
项和记为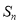 ,
, ,
,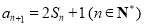 .
.
(Ⅰ)当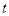 为何值时,数列
为何值时,数列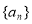 是等比数列;
是等比数列;
(Ⅱ)在(I)的条件下,若等差数列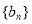 的前
的前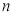 项和
项和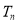 有最大值,且
有最大值,且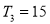 ,
,
又 ,
,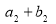 ,
, 成等比数列,求
成等比数列,求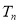 .
.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(文)试卷(解析版) 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-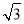 sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com