
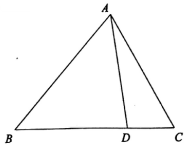
 在△ABC中,D为BC边上一点,AD=BD,AC=4,BC=5.
在△ABC中,D为BC边上一点,AD=BD,AC=4,BC=5.分析 (1)利用余弦定理表示出AB,再利用正弦定理即可求出外接圆半径R;
(2)根据正弦定理余弦定理和三角形面积公式即可求出
解答 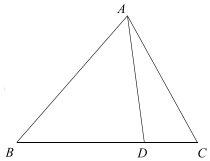 解:(1)由余弦定理,得AB2=BC2+AC2-2BC•AC•cos60°=21,
解:(1)由余弦定理,得AB2=BC2+AC2-2BC•AC•cos60°=21,
解得$AB=\sqrt{21}$.
由正弦定理得,$\frac{AB}{sinC}=\frac{{\sqrt{21}}}{{sin{{60}°}}}=2R,R=\sqrt{7}$.
(2)设CD=x,则BD=5-x,AD=5-x,
∵AD=BD,∴∠B=∠DAB.
∴∠CAD=∠CAB-∠DAB=∠CAB-∠B=θ.
∵$tanθ=\frac{{\sqrt{15}}}{7}$,∴$0<θ<\frac{π}{2},cosθ=\frac{7}{8}$.
∴$cos∠CAD=cosθ=\frac{{A{D^2}+A{C^2}-C{D^2}}}{2AD•AC}$,
即$\frac{{{{(5-x)}^2}+{4^2}-{x^2}}}{2×4×(5-x)}=\frac{7}{8}$,解得x=2.
∴BD=AD=3.
∵$\frac{AD}{sinC}=\frac{CD}{sin∠CAD}$,
∴$sinC=\frac{3}{2}sinθ=\frac{{3\sqrt{15}}}{16}$.
∴${S_{△ABC}}=\frac{1}{2}AC•BC•sinC=\frac{1}{2}×4×5×\frac{{3\sqrt{15}}}{16}=\frac{{15\sqrt{15}}}{8}$.
点评 此题考查了正弦、余弦定理,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}$ | B. | $\frac{9}{2}$ | C. | -8 | D. | $\frac{17}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com