
【题目】用计算机随机产生的有序二元数组(x,y)满足﹣1≤x≤1,﹣1≤y≤1.
(1)若x,y∈Z,求事件“x2+y2≤1”的概率.
(2)求事件“x2+y2>1”的概率.
【答案】
(1)解:x∈{﹣1,0,1}; y∈{﹣1,0,1}
∴基本事件总数n=3×3=9
∵x2+y2≤1,
∴所有事件(﹣1,0)(0,0)(0,1),m=3
∴所求概率为 ![]() =
= ![]()
(2)解:试验发生包含的事件对应的集合是Ω={(x,y)|﹣1<x<1,﹣1<y<1},
它的面积是2×2=4,
满足条件的事件对应的集合是A={(x,y)|﹣1<x<1,﹣1<y<1,x2+y2>1}
集合A对应的图形的面积是边长为2的正方形内部,且圆的外部,面积是4﹣π
∴根据几何概型的概率公式得到P= ![]()
【解析】(1)先确定基本事件总数n=3×3=9,满足x2+y2≤1,所有事件(﹣1,0)(0,0)(0,1),m=3,即可求得事件“x2+y2≤1”的概率;(2)本题是一个几何概型,试验发生包含的事件对应的集合是Ω={(x,y)|﹣1<x<1,﹣1<y<1},满足条件的事件对应的集合是A={(x,y)|﹣1<x<1,﹣1<y<1,x2+y2>1},做出两个集合对应的图形的面积,根据几何概型概率公式得到结果.
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲、乙、丙面试合格的概率分别是 ![]() ,
, ![]() ,
, ![]() ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一点在直线上从时刻t=0(s)开始以速度v(t)=t2﹣4t+3(m/s)运动,求:
(1)在t=4s时的位置;
(2)在t=4s的运动路程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为
(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为
(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1 , CC1上,且C1F= ![]() C1C,BE=λBB1 , 0<λ<1.
C1C,BE=λBB1 , 0<λ<1. 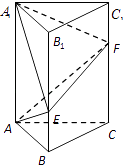
(1)当λ= ![]() 时,求异面直线AE与A1F所成角的大小;
时,求异面直线AE与A1F所成角的大小;
(2)当直线AA1与平面AEF所成角的正弦值为 ![]() 时,求λ的值.
时,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论: ①函数 ![]() 的值域是(0,+∞);
的值域是(0,+∞);
②直线2x+ay﹣1=0与直线(a﹣1)x﹣ay﹣1=0平行,则a=﹣1;
③过点A(1,2)且在坐标轴上的截距相等的直线的方程为x+y=3;
④若圆柱的底面直径与高都等于球的直径,则圆柱的侧面积等于球的表面积.
其中正确的结论序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com