
���� �������ú���g��x��=k��x��-$\frac{1}{2}x$Ϊż���������k��-1��=0�����a��b��c����������k��x���ı���ʽ��
�������0$��\frac{{x}_{1}}{{x}_{2}}��\frac{1}{2}$��y=��x1-x2���ա䣨$\frac{{x}_{1}+{x}_{2}}{2}$��=$\frac{2��\frac{{x}_{1}}{{x}_{2}}-1��}{\frac{{x}_{1}}{{x}_{2}}+1}$-$ln\frac{{x}_{1}}{{x}_{2}}$���ٻ�Ԫ�����캯����������ȷ�������ĵ����ԣ������������Сֵ�����ɵó����ۣ�
��� �⣺��������֪�ɵ�k��x��=ax2+bx+c��
�ߺ���g��x��=k��x��-$\frac{1}{2}x$Ϊż������
��ax2-bx+c+$\frac{1}{2}$x=ax2+bx+c-$\frac{1}{2}x$��
�ࣨa-$\frac{1}{2}$��x2+$\frac{1}{2}x$+c-$\frac{1}{2}$��0�������
��$\left\{\begin{array}{l}{a-\frac{1}{2}��0}\\{\frac{1}{4}-4��a-\frac{1}{2}����c-\frac{1}{2}����0}\end{array}\right.$
��a=c=$\frac{1}{4}$��
��k��-1��=0�����k��x��=$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{1}{4}$��
�����ɣ��ã�f��x��=$\frac{1}{12}{x}^{3}$+$\frac{1}{4}$x2+$\frac{1}{4}$x��
��h��x��=2lnx+x2+3-2mx��
��h�䣨x��=$\frac{2��{x}^{2}-mx+1��}{x}$��
������á�=m2-4��0��x1+x2=m��x1x2=1
��m$��\frac{3\sqrt{2}}{2}$��
����0$��\frac{{x}_{1}}{{x}_{2}}��\frac{1}{2}$��
��x1��x2��x1��x2��ǡΪ�գ�x��=lnx-sx2-tx����㣬
����룬��ʽ����ã�$ln\frac{{x}_{1}}{{x}_{2}}$-s��x1-x2����x1+x2��-t��x1-x2��=0��
�֦ա䣨x��=$\frac{1}{x}$-2sx-t���Ӷ�y=��x1-x2���ա䣨$\frac{{x}_{1}+{x}_{2}}{2}$��=$\frac{2��\frac{{x}_{1}}{{x}_{2}}-1��}{\frac{{x}_{1}}{{x}_{2}}+1}$-$ln\frac{{x}_{1}}{{x}_{2}}$��
��n=$\frac{{x}_{1}}{{x}_{2}}$��0$��n��\frac{1}{2}$����
��y=��x1-x2���ա䣨$\frac{{x}_{1}+{x}_{2}}{2}$��=$\frac{2��n-1��}{n+1}$-lnn��0$��n��\frac{1}{2}$������ΪM��n����
M�䣨n��=$\frac{-��n-1��^{2}}{n��n+1��^{2}}$��0
��M��n���ڣ�0��$\frac{1}{2}$]�ϵ����ݼ���
��M��n��min=ln2-$\frac{2}{3}$��
��y=��x1-x2���ա䣨$\frac{{x}_{1}+{x}_{2}}{2}$������СֵΪln2-$\frac{2}{3}$��
���� ���⿼�鵼��֪ʶ���ۺ����ã����麯�������ʣ����鹹�캯�����������ã��Ѷȴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{4}$ | B�� | $\frac{��}{2}$ | C�� | $\frac{3��}{4}$ | D�� | $\frac{��}{4}$��$\frac{3��}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | 8 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
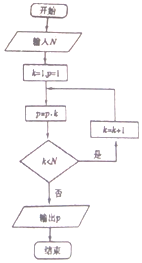
| A�� | 120 | B�� | 720 | C�� | 1440 | D�� | 5040 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{n+1}{2��n+2��}$ | B�� | $\frac{3}{4}$-$\frac{n+1}{2��n+2��}$ | C�� | $\frac{3}{4}$-$\frac{1}{2}$��$\frac{1}{n+1}$+$\frac{1}{n+2}$�� | D�� | $\frac{3}{2}$-$\frac{1}{n+1}$+$\frac{1}{n+2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
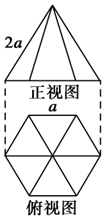 ��ͼ��һ�������������ͼ����ͼ��
��ͼ��һ�������������ͼ����ͼ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com