
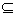 A,card(B)=12(card(B)指集合B中的元素的个数),且存在a,b∈B,b<a,b|a,则称B为“和谐集”。求最大的m∈A,使含m的集合A的有12个元素的任意子集为“和谐集”,并说明理由。
A,card(B)=12(card(B)指集合B中的元素的个数),且存在a,b∈B,b<a,b|a,则称B为“和谐集”。求最大的m∈A,使含m的集合A的有12个元素的任意子集为“和谐集”,并说明理由。  ;
;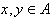 ,
,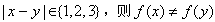 ,
,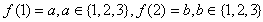 ,
,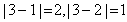 ,
,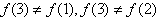 。
。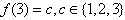 ,这里
,这里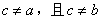 ,
,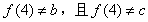 ,
,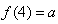 ,
,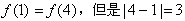 ,与已知矛盾;
,与已知矛盾;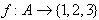 ,
,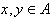 ,
,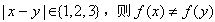 。
。 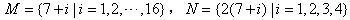 ,
,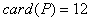 ,
,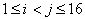 ,不存在n≥3,使得
,不存在n≥3,使得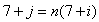 成立,
成立,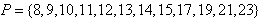 ;
;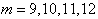 时,存在含m的集合A的有12个元素的子集为非“和谐集”,因此m≤7;
时,存在含m的集合A的有12个元素的子集为非“和谐集”,因此m≤7;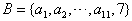 ,
,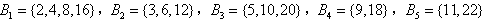 ,
, ,
,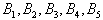 每个集合中的元素都是倍数关系,
每个集合中的元素都是倍数关系, 的情况,也即B′中5个元素全都是B的元素,B中剩下6个元素必须从
的情况,也即B′中5个元素全都是B的元素,B中剩下6个元素必须从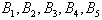 这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,即集合B中至少有两个元素存在倍数关系;
这5个集合中选取6个元素,那么至少有一个集合有两个元素被选,即集合B中至少有两个元素存在倍数关系;

科目:高中数学 来源: 题型:
(08年黄冈中学三模理)设![]() 的极小值为
的极小值为![]() ,其导函数
,其导函数![]() 的图像是经过点
的图像是经过点![]() 开口向上的抛物线,如图所示.
开口向上的抛物线,如图所示.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若直线![]() 与函数
与函数![]() 有三个交点,
有三个交点,
求实数![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| k |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.C20103个 | B.A32010个 | C.2A21005个 | D.2C21005个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com