
【题目】若过点![]() 可作曲线
可作曲线![]() 的切线恰有两条,则
的切线恰有两条,则![]() 的最小值为__________
的最小值为__________
【答案】![]()
【解析】
求出f(x)的导数,设切点(x0,f(x0)),求得切线的方程,代入切点,整理化简可得2x03﹣(3+3a)x02+6ax0+b=0(*)由条件切线恰有两条,方程(*)恰有两根.令u(x)=2x3﹣(3+3a)x2+6ax+b,求出导数,求得极值点,令其中一个极值为0,可得3a+b=1,运用乘1法和基本不等式,计算即可得到所求最小值.
f′(x)=3x2﹣6x,
过点P(a,b)作曲线的切线,
设切点(x0,f(x0)),则切线方程为:y﹣b=(3x02﹣6x0)(x﹣a),
将(x0,f(x0))代入得:f(x0)=(3x02﹣6x0)(x0﹣a)+b=x03﹣3x02,
即2x03﹣(3+3a)x02+6ax0+b=0(*)
由条件切线恰有两条,方程(*)恰有两根.
令u(x)=2x3﹣(3+3a)x2+6ax+b,u′(x)=6x2﹣(6+6a)x+6a=6(x﹣a)(x﹣1),
可得u(1)=0或u(a)=0,
即有3a+b=1或b=a3﹣3a2(舍去),
则![]() =(3a+b)(
=(3a+b)(![]() )=4+
)=4+![]() +≥4+2
+≥4+2![]() =4+2
=4+2![]() ,
,
当且仅当b=![]() a=
a=![]() 时,取得等号.
时,取得等号.
即有![]() 的最小值为4+2
的最小值为4+2![]() ,
,
故答案为:4+2![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某学校为了解学生假期参与志愿服务活动的情况,随机调查了![]() 名男生,
名男生,![]() 名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
名女生,得到他们一周参与志愿服务活动时间的统计数据如右表(单位:人):
超过 | 不超过 | |
男 |
|
|
女 |
|
|
(1)能否有![]() 的把握认为该校学生一周参与志愿服务活动时间是否超过
的把握认为该校学生一周参与志愿服务活动时间是否超过![]() 小时与性别有关?
小时与性别有关?
(2)以这![]() 名学生参与志愿服务活动时间超过
名学生参与志愿服务活动时间超过![]() 小时的频率作为该事件发生的概率,现从该校学生中随机抽查
小时的频率作为该事件发生的概率,现从该校学生中随机抽查![]() 名学生,试估计这
名学生,试估计这![]() 名学生中一周参与志愿服务活动时间超过
名学生中一周参与志愿服务活动时间超过![]() 小时的人数.
小时的人数.
附:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: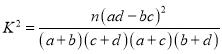
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为5.
的距离为5.
(1)求![]() 与
与![]() 的值;
的值;
(2)设动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,问:在
两点,问:在![]() 轴上是否存在与
轴上是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex![]() (x﹣a)2+4.
(x﹣a)2+4.
(1)若f(x)在(﹣∞,+∞)上单调递增,求a的取值范围;
(2)若x≥0,不等式f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com