
【题目】已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)=![]() 是奇函数.
是奇函数.
(1)确定y=f(x)和y=g(x)的解析式;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意x∈[-5,-1],都有f(1-x)+f(1-2x)>0成立,求x的取值范围.
【答案】(1)f(x)=![]() ,g(x)=2x;(2)见解析;(3)[2,3].
,g(x)=2x;(2)见解析;(3)[2,3].
【解析】
(1)由题意可设![]() ,代入条件可得函数解析式,从而得f(x);
,代入条件可得函数解析式,从而得f(x);
(2)任取x1,x2∈R,x1<x2,化简f(x1)-f(x2)与0比较大小即可得单调性;
(3)由函数为奇函数可得f(1-x)>f(2x-1),,结合单调性和定义域可得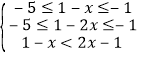 ,从而得解.
,从而得解.
(1)设![]() ,
,
∵g(3)=a3=8,∴a=2,∴g(x)=2x,
∴f(x)=![]() ,
,
∵f(x)是奇函数,∴f(-1)+f(1)=0,即![]() ,解得m=2.
,解得m=2.
经检验,当m=2时,f(x)=![]() 为奇函数,
为奇函数,
∴f(x)=![]() ;
;
(2)任取x1,x2∈R,x1<x2,
则f(x1)-f(x2)=![]() =
=![]() .
.
∵x1<x2,
∴2x2-2x1>0,
又∵1+2x1>0,1+2x2>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)是定义在R上的减函数;
(3)∵f(1-x)+f(1-2x)>0,且f(x)为奇函数,
∴f(1-x)>f(2x-1),
∴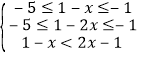 ,
,
解得2≤x≤3,
∴x的取值范围是[2,3].


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】设F1,F2分别是椭圆C:![]() (a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(a>b>0)的左,右焦点,M是C上一点且MF2与x轴垂直,直线MF1与C的另一个交点为N.
(1)若直线MN的斜率为![]() ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且|MN|=5|F1N|,求a,b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2
(t为参数,t≠0),其中0≤α<π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=2 ![]() cosθ.
cosθ.
(1)求C2与C3交点的直角坐标;
(2)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,PA⊥底面ABCD,E是棱PD上异于P,D的动点.设 ![]() =m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( )
=m,则“0<m<2”是三棱锥C﹣ABE的体积不小于1的( ) 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别是a,b,c,已知c=6,sinA﹣sinC=sin(A﹣B).若1≤a≤6,则sinC的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|)。
(1)求实数a,b的值;
(2)若不等式f(2k)>1成立,求实数k的取值范围;
(3)定义在[p,q]上的函数![]() (x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式
(x),设p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l将区间[p,q]任意划分成n个小区间,如果存在一个常数M>0,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() (x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
(x)为在[p,q]上的有界变差函数。试判断函数f(x)是否为在[0,4]上的有界变差函数?若是,求M的最小值;若不是,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|7﹣6x≤0},集合B={x|y=lg(x+2)},则(UA)∩B等于( )
A.(﹣2, ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.[﹣2, ![]() )
)
D.(﹣2,﹣ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com