
【题目】已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点P(4,m)到焦点的距离为6.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线y=kx﹣2相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
【答案】解:(Ⅰ)由题意设抛物线方程为y2=2px,其准线方程为x=﹣ ![]() ,
,
∵P(4,m)到焦点的距离等于A到其准线的距离,
∴4+ ![]() ∴p=4
∴p=4
∴抛物线C的方程为y2=8x
(Ⅱ)由 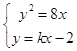 消去y,得 k2x2﹣(4k+8)x+4=0
消去y,得 k2x2﹣(4k+8)x+4=0
∵直线y=kx﹣2与抛物线相交于不同两点A、B,则有k≠0,△=64(k+1)>0,解得k>﹣1且k≠0,
又 ![]() =2,
=2,
解得 k=2,或k=﹣1(舍去)
∴k的值为2.
【解析】(Ⅰ)由题意设:抛物线方程为y2=2px,其准线方程为x=﹣ ![]() ,根据抛物线的大于可得:4+
,根据抛物线的大于可得:4+ ![]() ,进而得到答案.(Ⅱ)联立直线与抛物线的方程得 k2x2﹣(4k+8)x+4=0,根据题意可得△=64(k+1)>0即k>﹣1且k≠0,再结合韦达定理可得k的值.
,进而得到答案.(Ⅱ)联立直线与抛物线的方程得 k2x2﹣(4k+8)x+4=0,根据题意可得△=64(k+1)>0即k>﹣1且k≠0,再结合韦达定理可得k的值.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣3,数列{bn}的前n项和Tn满足 ![]() =
= ![]() +1且b1=1.
+1且b1=1.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前n项和Pn;
,求数列{cn}的前n项和Pn;
(3)数列{Sn}中是否存在不同的三项Sp , Sq , Sr , 使这三项恰好构成等差数列?若存在,求出p,q,r的关系;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数有( )
(1)数列{an},{bn}都是等差数列,则数列{an+bn}也一定是等差数列;
(2)数列{an},{bn}都是等比数列,则数列{an+bn}也一定是等比数列;
(3)等差数列{an}的首项为a1 , 公差为d,取出数列中的所有奇数项,组成一个新的数列,一定还是等差数列;
(4) G为a,b的等比中项G2=ab.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若 ![]() ,
, ![]() ,
, ![]() 为同一平面内互不共线的三个单位向量,并满足
为同一平面内互不共线的三个单位向量,并满足 ![]() +
+ ![]() +
+ ![]() =
= ![]() ,且向量
,且向量 ![]() =x
=x ![]() +
+ ![]()
![]() +(x+
+(x+ ![]() )
) ![]() (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求 ![]() 与
与 ![]() 所成角的大小;
所成角的大小;
(2)记f(x)=| ![]() |,试求f(x)的单调区间及最小值.
|,试求f(x)的单调区间及最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司过去五个月的广告费支出x与销售额y(单位:万元)之间有下列对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y |
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中y的第一个数据丢失.已知y对x呈线性相关关系,且回归方程为 ![]() =6.5x+17.5,则下列说法:
=6.5x+17.5,则下列说法:
①销售额y与广告费支出x正相关;
②丢失的数据(表中 ![]() 处)为30;
处)为30;
③该公司广告费支出每增加1万元,销售额一定增加6.5万元;
④若该公司下月广告投入8万元,则销售额为70万元.
其中,正确说法有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,则该几何体的外接球的表面积是( ) 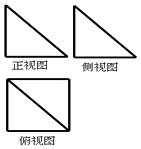
A.![]()
B.4 ![]() π
π
C.12π
D.![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点,焦点在x轴上的椭圆,离心率为 ![]() 且过点(
且过点( ![]() ,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
,0),过定点C(﹣1,0)的动直线与该椭圆相交于A、B两点.
(1)若线段AB中点的横坐标是﹣ ![]() ,求直线AB的方程;
,求直线AB的方程;
(2)在x轴上是否存在点M,使 ![]() 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com