
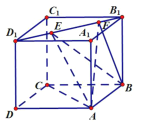
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,则下列结论中正确的是__________.
,则下列结论中正确的是__________.
①![]() 平面
平面![]() ;
;
②平面![]() 平面
平面![]() ;
;
③三棱锥![]() 的体积为定值;
的体积为定值;
④存在某个位置使得异面直线![]() 与
与![]() 成角
成角![]() .
.
【答案】①②③④
【解析】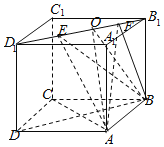
由正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=![]() ,知:
,知:
在①中,由EF∥BD,且EF平面ABCD,BD平面ABCD,得EF∥平面ABCD,故①正确;
在②中,连接BD,由AC⊥BD,AC⊥DD1,可知AC⊥面BDD1B1,
而BE面BDD1B1,BF面BDD1B1,∴AC⊥平面BEF,
∵AC平面ACF,∴面ACF⊥平面BEF,故②正确;
在③中,三棱锥E﹣ABF的体积与三棱锥A﹣BEF的体积相等,
三棱锥A﹣BEF的底面积和高都是定值,故三棱锥E﹣ABF的体积为定值,故③正确;
在④中,令上底面中心为O,当E与D1重合时,此时点F与O重合,
则两异面直线所成的角是∠OBC1,可求解∠OBC1=300,
故存在某个位置使得异面直线AE与BF成角30°,故④正确.
故答案为:①②③④.


科目:高中数学 来源: 题型:
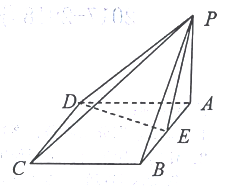
【题目】如图,四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益
,乙城市收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足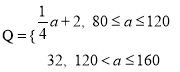 ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合A、B满足以下四个条件:
①A∪B={1,2,3,4,5,6,7};②A∩B=;③A中的元素个数不是A中的元素;④B中的元素个数不是B中的元素.
若集合A含有2个元素,则满足条件的A有个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间.
问:离家前不能看到报纸(称事件![]() )的概率是多少?(须有过程)
)的概率是多少?(须有过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com