
 、
、 两点的坐标分别为A
两点的坐标分别为A B
B
 。 (1)求
。 (1)求 的表达式;(2)若
的表达式;(2)若 (
( 为坐标原点),求
为坐标原点),求 的值;
的值; (
( ),求函数
),求函数 的最小值。
的最小值。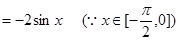 ;(2)
;(2)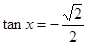 ;(3)当
;(3)当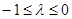 时,
时, 的最小值为
的最小值为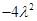 ,此时
,此时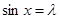 ;当
;当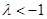 时,
时, 的最小值为
的最小值为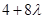 ,此时
,此时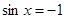 ;
;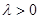 时,
时, 的最小值为0,此时
的最小值为0,此时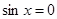
 ,然后将利用二倍角公式化为单角的三角函数关系式,分子和分母分别除以该角的余弦值的平方,得到结论。
,然后将利用二倍角公式化为单角的三角函数关系式,分子和分母分别除以该角的余弦值的平方,得到结论。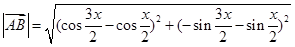
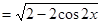
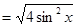
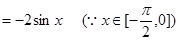
 , ∴
, ∴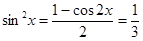 ,
,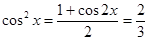
 , ∴
, ∴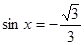 ,
,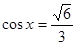 .∴
.∴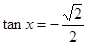 。
。 =
= =
=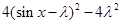
 ,∴
,∴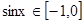
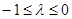 时,
时, 的最小值为
的最小值为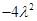 ,此时
,此时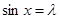 ;
;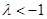 时,
时, 的最小值为
的最小值为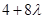 ,此时
,此时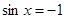 ;
;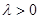 时,
时, 的最小值为0,此时
的最小值为0,此时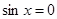


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com