解:(Ⅰ)当a=1时,f′(x)=2x-3+

=
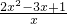
=
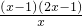
,…2分
当0<x

时,f′(x)>0;当

<x<1时,f′(x)<0;当x>1时,f′(x)>0.
所以当x=1时,函数f(x)取极小值f(1)=-2,…5分;
(Ⅱ)当a=-1时,f′(x)=2x-1-

(x>0),所以切线的斜率
k=2m-1-

=
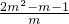
=

=
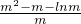
,整理可得m
2+lnm-1=0,
显然m=1是方程的解,又因为函数y=x
2+lnx-1在(0,+∞)上是增函数,
所以方程有唯一的实数解,即m=1,…10分;
(Ⅲ)当a=8时,函数y=f(x)在其图象上一点P(x
0,y
0)处的切线方程为:
h(x)=
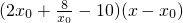
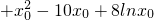
,
设F(x)=f(x)-h(x),则F(x
0)=0,F′(x)=f′(x)-h′(x)
=(
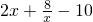
)-(
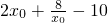
)=

(x-x
0)(x-
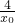
)
若0<x
0<2,F(x)在(x
0,
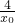
)上单调递减,所以当x∈(x
0,
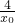
)时,
F(x)<F(x
0)=0,此时
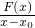
<0,
若x
0>2,F(x)在(
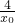
,x
0)上单调递减,所以当x∈(
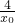
,x
0)时,
F(x)>F(x
0)=0,此时
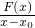
<0,
所以y=f(x)在(0,2)和(2,+∞)上不存在“转点”,
若x
0=2时,F′(x)=
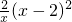
,即F(x)在(0,+∞)上是增函数,
当x>x
0时,F(x)>F(x
0)=0,当x<x
0时,F(x)<F(x
0)=0,
故点P(x
0,f(x
0))为“转点”,
故函数y=f(x)存在“转点”,且2是“转点”的横坐标,…15分
分析:(Ⅰ)把a=1代入可得函数的导数,进而可得单调区间,可得极小值;
(Ⅱ)把a=-1代入,可得切线斜率,由斜率公式还可得斜率,由等式可得m=1是唯一的实数解;
(Ⅲ)针对新定义,构造函数F(x)=f(x)-h(x),求其导数,分0<x
0<2,x
0>2,x
0=2三种情况进行讨论,可得结论.
点评:本题考查利用导数研究函数的单调性和极值,涉及新定义,属中档题.

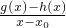 >0在D内恒成立,则称P为函数y=g(x)的“转点”.当a=8时,试问函数y=f(x)是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=g(x)的“转点”.当a=8时,试问函数y=f(x)是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由. =
=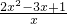 =
=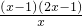 ,…2分
,…2分 时,f′(x)>0;当
时,f′(x)>0;当 <x<1时,f′(x)<0;当x>1时,f′(x)>0.
<x<1时,f′(x)<0;当x>1时,f′(x)>0. (x>0),所以切线的斜率
(x>0),所以切线的斜率 =
=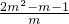 =
= =
=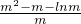 ,整理可得m2+lnm-1=0,
,整理可得m2+lnm-1=0,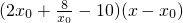
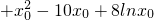 ,
,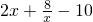 )-(
)-(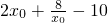 )=
)= (x-x0)(x-
(x-x0)(x-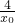 )
)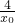 )上单调递减,所以当x∈(x0,
)上单调递减,所以当x∈(x0,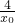 )时,
)时,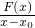 <0,
<0,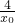 ,x0)上单调递减,所以当x∈(
,x0)上单调递减,所以当x∈(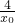 ,x0)时,
,x0)时,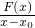 <0,
<0,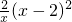 ,即F(x)在(0,+∞)上是增函数,
,即F(x)在(0,+∞)上是增函数,

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<