
【题目】设函数![]()
(1)当![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(2)设![]() 在
在![]() 上有两个极值点
上有两个极值点![]() .
.
(A)求实数![]() 的取值范围;
的取值范围;
(B)求证: ![]() .
.
【答案】(1)![]() ;(2)(A)
;(2)(A)![]() ;(B)证明见解析;
;(B)证明见解析;
【解析】试题分析:(1)构造函数![]() ,求导数分
,求导数分![]() ,
, ![]() ,
, ![]() ,
, ![]() 出函数的最值即可,
出函数的最值即可,
(2)函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,即导函数g′(x)有两个不同的实数根,对a进行分类讨论,不妨设
,即导函数g′(x)有两个不同的实数根,对a进行分类讨论,不妨设![]() ,则
,则![]() ,构造函数
,构造函数![]() ,
, ![]() .,利用函数
.,利用函数![]() 的单调性证明不等式.
的单调性证明不等式.
试题解析:
解:(1)∵![]() ,且
,且![]() ,
,
∴![]() .
.
令![]() ,则
,则![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
∴![]() 时,
时, ![]() ,不合题意.
,不合题意.
②当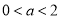 时,
时, ![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
∴![]() ,
, ![]() ,不合题意.
,不合题意.
③当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 在
在![]() 上为单调递减函数.
上为单调递减函数.
∴![]() 时,
时, ![]() ,不合题意.
,不合题意.
④当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 在
在![]() 上为单调递增函数.
上为单调递增函数.
![]() ,
, ![]() ,
, ![]() 在
在![]() 上为单调递减函数.
上为单调递减函数.
∴![]() ,符合题意.
,符合题意.
综上, ![]() .
.
(2)![]() ,
, ![]() .
.
![]() .
.
令![]() ,则
,则![]()
由已知![]() 在
在![]() 上有两个不等的实根.
上有两个不等的实根.
(A)①当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为单调递增函数,不合题意.
上为单调递增函数,不合题意.
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上为单调递减函数,不合题意.
上为单调递减函数,不合题意.
③当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以, ![]() ,
, ![]() ,
, ![]() ,解得
,解得![]() .
.
(B)由已知![]() ,
, ![]() ,
,
∴![]() .
.
不妨设![]() ,则
,则![]() ,则
,则![]()
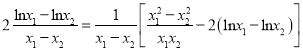
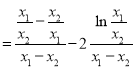 .
.
令![]() ,
, ![]() .
.
则![]() ,∴
,∴![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
∴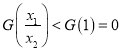
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(A)![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代太极图是一种优美的对称图.如果一个函数的图像能够将圆的面积和周长分成两个相等的部分,我们称这样的函数为圆的“太极函数”.下列命题中错误命题的个数是( )
![]() 对于任意一个圆其对应的太极函数不唯一;
对于任意一个圆其对应的太极函数不唯一;
![]() 如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
![]() 圆
圆![]() 的一个太极函数为
的一个太极函数为![]() ;
;
![]() 圆的太极函数均是中心对称图形;
圆的太极函数均是中心对称图形;
![]() 奇函数都是太极函数;
奇函数都是太极函数;
![]() 偶函数不可能是太极函数.
偶函数不可能是太极函数.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马, 田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个服装店经营某种服装,在某周内获纯利润y/元与该周每天销售这种服装件数x/件之间的数据如表:
X | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
已知x12+x22+…+x72=280,x1y1+x2y2+…+x7y7=3487.
(1)求 ![]() ,
, ![]() ;
;
(2)画出散点图;
(3)判断纯利润y与每天销售件数x之间是否线性相关,如果线性相关,求出线性回归方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15. 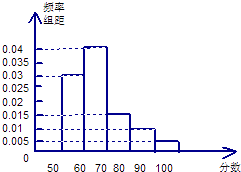
(1)求成绩在50~70分的频率是多少;
(2)求这三个年级参赛学生的总人数是多少;
(3)求成绩在80~100分的学生人数是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为( )
A.﹣ ![]() 或﹣
或﹣ ![]()
B.﹣ ![]() 或﹣
或﹣ ![]()
C.﹣ ![]() 或﹣
或﹣ ![]()
D.﹣ ![]() 或﹣
或﹣ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com