
����Ŀ��һ�����������ɸ���С��ͬ�ĺ�����ͺ�����֪�Ӵ�����������1���õ�����ĸ����� ![]() ���Ӵ�����������2�������ٵõ�1������ĸ�����
���Ӵ�����������2�������ٵõ�1������ĸ����� ![]() �� ���������й���10����
�� �����������10����
��i�������ĸ�����
��ii���Ӵ�����������3���ǵõ�����ĸ���Ϊ�Σ�����������ε���ѧ����E�Σ�
������֤���Ӵ�����������2�������ٵõ�1������ĸ��ʲ����� ![]() ����ָ������������ɫ����������٣�
����ָ������������ɫ����������٣�
���𰸡��⣺����i���ǡ��Ӵ�����������2�������ٵõ�1������Ϊ�¼�A�� ����а������Ϊx����P��A��=1�� ![]() =
= ![]() ��
��
���x=5������������5����
��ii����������ε�ȡֵΪ0��1��2��3��
P����=0��= ![]() =
= ![]() =
= ![]() ��
��
P����=1��= ![]() =
= ![]() ��
��
P����=2��= ![]() ��
��
P����=3��= ![]() =
= ![]() =
= ![]() ��
��
��εķֲ���Ϊ��
�� | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E��= ![]() =
= ![]() ��
��
֤���������������n��������y������
�����⣬��y= ![]() n��
n��
��2y��n��2y��n��1��
�� ![]() ��
��
�ǡ��Ӵ�������ȡ��������������1������Ϊ�¼�B��
��P��B��= ![]() ��
��
�����ĸ����Ⱥ���࣬����������� ![]() �������������
������������� ��
�ʴ��к����������
����������������а������Ϊx���ɶ����¼����ʼ��㹫ʽ�ã�1�� ![]() =
= ![]() ���ɴ�����������������ii����������ε�ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ��������������ε���ѧ����E�Σ����������n��������y�����������⣬��y=
���ɴ�����������������ii����������ε�ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ��������������ε���ѧ����E�Σ����������n��������y�����������⣬��y= ![]() n���Ӷ�2y��n��2y��n��1������
n���Ӷ�2y��n��2y��n��1������ ![]() ���ɴ���֤���Ӵ�����������2�������ٵõ�1������ĸ��ʲ�����
���ɴ���֤���Ӵ�����������2�������ٵõ�1������ĸ��ʲ����� ![]() �����õ�����������ɫ����������٣�
�����õ�����������ɫ����������٣�
�����㾫�������ڱ��⿼�����ɢ�������������ֲ��У���Ҫ�˽����������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в��ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() ��
�� ![]() �ļн�Ϊ120�㣬��|
�ļн�Ϊ120�㣬��| ![]() |=4��|
|=4��| ![]() |=2����
|=2����
��1���� ![]() ��2
��2 ![]() ����
���� ![]() +
+ ![]() ����
����
��2��|3 ![]() ��4
��4 ![]() |��
|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ķ�����ΪR����f��x����Ϊ��ֵ���������������⣺ �ٺ���g��x��=f��x��+f����x��һ����ż������
����������x��R����f��x��+f��2��x��=0����f��x������2Ϊ���ڵ����ں�����
����f��x�����溯�����Ҷ�������x��R������f��x��+f��2+x��=0����f��x����ͼ��ĶԳ��᷽��Ϊx=2n+1��n��Z����
�ܶ��������x1 �� x2��R����x1��x2 �� �� ![]() ��0���������f��x��ΪR�ϵ���������
��0���������f��x��ΪR�ϵ���������
����������ȷ���������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�о�ѧ�������������������������ʱ��Ĺ�ϵ���Ը�У200������ѧ���Ŀ�����������ƽ��ÿ���˶���ʱ����е��飬�������ƽ��ÿ�������ʱ�䵥λ�����ӣ�
ƽ��ÿ����� | [0��10�� | [10��20�� | [20��30�� | [30��40�� | [40��50�� | [50��60�� |
������ | 20 | 36 | 44 | 50 | 40 | 10 |
��ѧ���վ�������������˶�ʱ����[40��60���ϵ�ѧ������Ϊ������������ꡱ��
������������������е�ͳ��������д����2��2����������ͨ�������ж��Ƿ����ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ������������ꡱ���Ա��йأ�
������������� | ����������� | �ϼ� | |
�� | |||
Ů | 20 | 110 | |
�ϼ� |
���������������õ���Ƶ����Ϊ���ʣ����ڴӸ�У����ѧ���У���ȡ3��ѧ�����DZ���ȡ��3��ѧ���еġ�����������ꡱѧ������ΪX����ÿ�γ�ȡ�Ľ����������ģ���X����ѧ�����ͷ��
�ο���ʽ�� ![]() ������n=a+b+c+d��
������n=a+b+c+d��
�ο����ݣ�
P��K2��k0�� | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У�
�� ![]() ��
�� ![]() ��
��![]() Ϊ����������ԭ��
Ϊ����������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ��������Ϊ���Ὠ��������ϵ����֪����
��������Ϊ���Ὠ��������ϵ����֪����![]() .
.
��1����![]() ����ͨ���̼�
����ͨ���̼�![]() ��ֱ�����귽�̣���˵�����Ƿֱ��ʾʲô���ߣ�
��ֱ�����귽�̣���˵�����Ƿֱ��ʾʲô���ߣ�
��2����![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
�� ![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����СֵΪ2����
����СֵΪ2����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
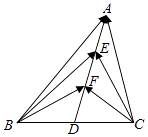
����Ŀ����ͼ���ڡ�ABC�У�D��BC���е㣬E��F��AD�ϵ��������ȷֵ㣬 ![]()
![]() =4��
=4�� ![]()
![]() =��1����
=��1���� ![]()
![]() ��ֵ�� ��
��ֵ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x����R����5Ϊ���ڵĿɵ�ż������������y=f��x����x=5�������ߵ�б��Ϊ�� ��
A.- ![]()
B.0
C.![]()
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������� ![]() ����0��x1��x2��1����
����0��x1��x2��1���� ![]() ����a��b�Ĵ�С��ϵ�ǣ� ��
����a��b�Ĵ�С��ϵ�ǣ� ��
A.a��b
B.a��b
C.a=b
D.b�Ĵ�С��ϵ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD������ΪO,�ı���ODEFΪ���Σ�ƽ��ODEF![]() ƽ��ABCD��DE=DA=DB=2
ƽ��ABCD��DE=DA=DB=2
��I����GΪDC���е㣬��֤��EG//ƽ��BCF;
��II����![]() ,������
,������![]() ������ֵ.
������ֵ.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com