
【题目】设向量 ![]() =(
=( ![]() sinx,sinx),
sinx,sinx), ![]() =(cosx,sinx),x∈(0,
=(cosx,sinx),x∈(0, ![]() ).
).
(1)若| ![]() |=|
|=| ![]() |,求x的值;
|,求x的值;
(2)设函数f(x)= ![]() ,求f(x)的最大值.
,求f(x)的最大值.
【答案】
(1)解:由|a|2=( ![]() sin x)2+(sin x)2=4sin2 x,
sin x)2+(sin x)2=4sin2 x,
|b|2=(cos x)2+(sin x)2=1.
及|a|=|b|,得4sin2 x=1.
又x∈(0, ![]() ),
),
从而sin x= ![]() ,
,
∴x= ![]()
(2)解:f(x)= ![]() =
= ![]() sin xcos x+sin2x=
sin xcos x+sin2x= ![]() sin 2x﹣
sin 2x﹣ ![]() cos 2x+
cos 2x+ ![]() =sin(2x﹣
=sin(2x﹣ ![]() )+
)+ ![]() ,
,
当x= ![]() ∈(0,
∈(0, ![]() )时,sin(2x﹣
)时,sin(2x﹣ ![]() )取最大值1.
)取最大值1.
∴f(x)的最大值为 ![]()
【解析】(1)根据| ![]() |=|
|=| ![]() |,建立方程关系,利用三角函数的公式即可求x的值(2)利用数量积的定义求出函数f(x)=
|,建立方程关系,利用三角函数的公式即可求x的值(2)利用数量积的定义求出函数f(x)= ![]() 的表达式,利用三角函数的图象和性质求f(x)的最大值.
的表达式,利用三角函数的图象和性质求f(x)的最大值.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sin2x+1﹣
sin2x+1﹣ ![]() .
.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,若f(x)≥log2t恒成立,求t的取值范围.
]时,若f(x)≥log2t恒成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
(1)写出S关于x的函数关系式;
(2)如何设计瓶子的尺寸(不考虑瓶壁的厚度),可以使表面积S最小,并求出最小值.
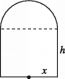
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+1)+![]() x2-ax+1(a>1).
x2-ax+1(a>1).
(1)求函数y=f(x)在点(0,f(0))处的切线方程;
(2)当a>1时,求函数y=f(x)的单调区间和极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com