
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额如下表:
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图,观察散点图,说明两个变量是否线性相关;
(2)用最小二乘法计算利润额y对销售额x的线性回归方程;
(3)当销售额为4千万元时,估计利润额的大小.
(参考公式: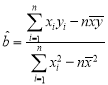 ,
,![]() )
)
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】设命题p:x0∈(1,+∞),使得5+|x0|=6.q:x∈(0,+∞),![]() +81x≥a.
+81x≥a.
(1)若a=9,判断命题¬p,p∨q,(¬p)∧(¬q)的真假,并说明理由;
(2)设命题r:x0∈R,x02+2x0+a-9≤0判断r成立是q成立的什么条件,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:

①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴,离心率为
轴,离心率为![]() ,且长轴长是短轴长的
,且长轴长是短轴长的![]() 倍.
倍.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 过椭圆
过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,若对满足条件的任意直线
两点,若对满足条件的任意直线![]() ,不等式
,不等式![]()
![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2018年第一季度五省GDP情况图,则下列描述中不正确的是( )
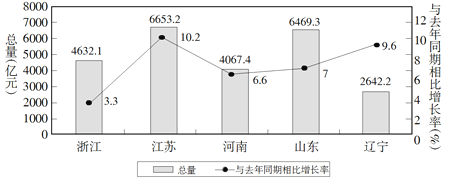
A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D. 去年同期河南省的GDP总量不超过4000亿元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中, ![]() ,
, ![]() 与
与![]() 交于
交于![]() 点,现将
点,现将![]() 沿
沿![]() 折起得到三棱锥
折起得到三棱锥![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
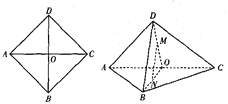
(1)求证: ![]() ;
;
(2)若三棱锥![]() 的最大体积为
的最大体积为![]() ,当三棱锥
,当三棱锥![]() 的体积为
的体积为![]() ,且二面角
,且二面角![]() 为锐角时,求二面角
为锐角时,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 右支上的一点
右支上的一点![]() ,经过点
,经过点![]() 的直线与双曲线
的直线与双曲线![]() 的两条渐近线分别相交于
的两条渐近线分别相交于![]() ,
,![]() 两点.若点
两点.若点![]() ,
,![]() 分别位于第一,四象限,
分别位于第一,四象限,![]() 为坐标原点.当
为坐标原点.当![]() 时,
时,![]() 为( )
为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与
与![]() 均为等边三角形,点
均为等边三角形,点![]() 为
为![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)试问在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com