练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数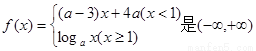上的减函数，那么a的取值范围是(   )

    A．（1，3）          B．（0，1）          C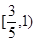．            D．（3，+∞）

     

    【答案】

    C

    【解析】

    试题分析：因为已知条件可知，函数y=f(x)在R上递减，则要满足每一个区间都是递减的，因此a-3>0,对数函数的底数0<a<1,同时要满足当x=1时，有(a-3)+4aloga1=0,这样联立不等式组可知解得实数a的范围为，选C.

    考点：本试题主要考查了分段函数的单调性的运用。

    点评：解决该试题的关键理解分段函数在整个实数集上单调的条件是每一段都是单调减，同时第一段的最小值大于等于第二段的最大值。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）满足f（x）+f'（0）-e-x=-1，函数g（x）=-λlnf（x）+sinx是区间[-1，1]上的减函数．
    （1）当x≥0时，曲线y=f（x）在点M（t，f（t））的切线与x轴、y轴围成的三角形面积为S（t），求S（t）的最大值；
    （2）若g（x）＜t2+λt+1在x∈[-1，1]时恒成立，求t的取值范围；
    （3）设函数h（x）=-lnf（x）-ln（x+m），常数m∈Z，且m＞1，试判定函数h（x）在区间[e-m-m，e2m-m]内的零点个数，并作出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数上的减函数，则a的取值范围是

           A．                B．                 C．（2，3）              D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)＝ln(ex＋a)(a为常数)是实数集R上的奇函数，函数g(x)＝λf(x)＋sinx是区间[－1,1]上的减函数．求实数λ取值的集合A.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)＝ex＋alnx的定义域是D，关于函数f(x)给出下列命题：

    ①对于任意a∈(0，＋∞)，函数f(x)是D上的减函数；

    ②对于任意a∈(－∞，0)，函数f(x)存在最小值；

    ③存在a∈(0，＋∞)，使得对于任意的x∈D，都有f(x)>0成立；

    ④存在a∈(－∞，0)，使得函数f(x)有两个零点．

    其中正确命题的序号是________(写出所有正确命题的序号)．

    查看答案和解析>>

    同步练习册答案