
【题目】如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8. 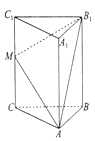
(1)求证:平面AB1M⊥平面A1ABB1;
(2)求平面AB1M与平面ABC所成二面角的正弦值.
【答案】
(1)证明:连结A1B,交AB1于点P,
∵三棱柱ABC﹣A1B1C1中,四边形ABB1A1是矩形,∴P是A1B的中点,
取AB的中点N,连结CN,PN,MP,
则NP∥CM,且NP=CM,∴四边形MCNP是平行四边形,
∴CN∥MP,
又AC=BC,∴CN⊥AB,
∵CC1⊥平面ABC,∴CC1⊥CN,
又AA1∥CC1,∴CN⊥AA1,
∴CN⊥平面A1ABB1,∴MP⊥平面A1ABB1,
∵MP平面AB1M,∴平面AB1M⊥平面A1ABB1.
(2)解:以N为原点,NA为x轴,CN为y轴,NP为z轴,建立空间直角坐标系,
∵AC=BC=5,AB=6,M是CC1中点,CC1=8,
∴A(3,0,0),M(0,﹣4,4),B1(﹣3,0,8),
![]() =(﹣3,﹣4,4),
=(﹣3,﹣4,4), ![]() =(﹣6,0,8),
=(﹣6,0,8),
设平面AB1M的法向量 ![]() =(x,y,z),
=(x,y,z),
则 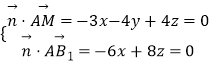 ,取x=4,得
,取x=4,得 ![]() =(4,0,3),
=(4,0,3),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
设平面AB1M与平面ABC所成二面角的平面角为θ,
则cosθ= 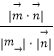 =
= ![]() ,sinθ=
,sinθ= ![]() =
= ![]() .
.
∴平面AB1M与平面ABC所成二面角的正弦值为 ![]() .
.
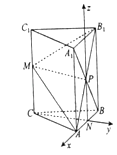
【解析】(1)连结A1B,交AB1于点P,取AB的中点N,连结CN,PN,MP,推导出四边形MCNP是平行四边形,从而CN∥MP,进而CC1⊥CN,由AA1∥CC1 , 知CN⊥AA1 , 从而CN⊥平面A1ABB1 , 进而MP⊥平面A1ABB1 , 由此能证明平面AB1M⊥平面A1ABB1 . (2)以N为原点,NA为x轴,CN为y轴,NP为z轴,建立空间直角坐标系,利用向量法能求出平面AB1M与平面ABC所成二面角的正弦值.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知抛物线C的方程C:y2="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于![]() ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[0,+∞)上的函数f(x)满足f(x)=2f(x+2),当x∈[0,2)时,f(x)=﹣2x2+4x.设f(x)在[2n﹣2,2n)上的最大值为an(n∈N*),且{an}的前n项和为Sn , 则Sn=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ln(x+a)(a∈R)有唯一的零点x0 , 则( )
A.﹣1<x0<﹣ ![]()
B.﹣ ![]() <x0<﹣
<x0<﹣ ![]()
C.﹣ ![]() <x0<0
<x0<0
D.0<x0< ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知h(x)=|2x﹣1|+m|x+3|(m>0),且h(x)的最小值是7. (Ⅰ)求m的值;
(Ⅱ)求出当h(x)取得最小值时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( ) 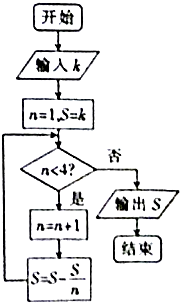
A.4.5
B.6
C.7.5
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n(n∈N*)项和为Sn , a3=3,且λSn=anan+1 , 在等比数列{bn}中,b1=2λ,b3=a15+1. (Ⅰ)求数列{an}及{bn}的通项公式;
(Ⅱ)设数列{cn}的前n(n∈N*)项和为Tn , 且 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆x2+y2=1上每一点的纵坐标不变,横坐标变为原来的 ![]() ,得曲线C. (Ⅰ)写出C的参数方程;
,得曲线C. (Ⅰ)写出C的参数方程;
(Ⅱ)设直线l:3x+y+1=0与C的交点为P1、P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若曲线f(x)= ![]() (e﹣1<x<e2﹣1)和g(x)=﹣x3+x2(x<0)上分别存在点A、B,使得△OAB是以原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,则实数a的取值范围是( )
(e﹣1<x<e2﹣1)和g(x)=﹣x3+x2(x<0)上分别存在点A、B,使得△OAB是以原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,则实数a的取值范围是( )
A.(e,e2)
B.(e, ![]() )
)
C.(1,e2)
D.[1,e)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com