
【题目】已知函数f(x)=x3+x,对任意的m∈[﹣2,2],f(mx﹣2)+f(x)<0恒成立,则x的取值范围为 .
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面为矩形,
中,底面为矩形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 上一点,
上一点, ![]() 为
为![]() 的中点.
的中点.
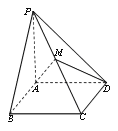
(1)在图中作出平面![]() 与
与![]() 的交点
的交点![]() ,并指出点
,并指出点![]() 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(2)求平面![]() 将四棱锥
将四棱锥![]() 分成上下两部分的体积比.
分成上下两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从4名男生,3名女生中选出三名代表,
(1)不同的选法共有多少种?
(2)至少有一名女生的不同的选法共有多少种?
(3)代表中男、女生都有的不同的选法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式f(x)= ![]() ﹣
﹣ ![]() (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两名同学参加定点投篮测试,已知两人投中的概率分别是![]() 和
和![]() ,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
(Ⅰ)若每人投球3次(必须投完),投中2次或2次以上,记为达标,求甲达标的概率;
(Ⅱ)若每人有4次投球机会,如果连续两次投中,则记为达标.达标或能断定不达标,则终止投篮.记乙本次测试投球的次数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com