
【题目】已知椭圆![]() 的右焦点与抛物线
的右焦点与抛物线![]() 的焦点重合,且该椭圆的离心率与双曲线
的焦点重合,且该椭圆的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】】试题分析: ![]() 由抛物线方程求得焦点坐标,求得
由抛物线方程求得焦点坐标,求得![]() 的值,由双曲线的离心率公式求得其离心率,则
的值,由双曲线的离心率公式求得其离心率,则![]() ,即可求得椭圆的半长轴
,即可求得椭圆的半长轴![]() 的值,则
的值,则![]() ,即可求得半短轴,即可求得椭圆的方程;
,即可求得半短轴,即可求得椭圆的方程;
⑵将直线方程代入椭圆方程,由韦达定理求得![]() ,则
,则![]() ,
,
![]() ,即可求得
,即可求得![]() 点坐标,由中点坐标公式求得
点坐标,由中点坐标公式求得![]() 点坐标,分类当
点坐标,分类当![]() 及当
及当![]() 时,由
时,由![]() ,根据向量的坐标表示,即可求得
,根据向量的坐标表示,即可求得![]() 的值
的值
解析:(I)抛物线的焦点坐标为![]() ,所以
,所以![]()
双曲线![]() 的离心率为
的离心率为![]() ,所以椭圆的离心率
,所以椭圆的离心率![]() ,
,
故椭圆的![]()
所以椭圆方程为: ![]()
(II)由(I)知![]() ,且直线
,且直线![]() 的斜率必存在,设斜率为
的斜率必存在,设斜率为![]() ,
,
则直线方程为: ![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,
,
联立方程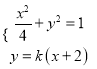 ,方程消去
,方程消去![]() 整理得:
整理得:
![]()
![]() 两点坐标满足上述方程,由韦达定理得
两点坐标满足上述方程,由韦达定理得![]() ,
,
所以![]() ,
, ![]()
所以![]() ,
, ![]() 的坐标为
的坐标为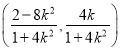 ,
,
线段![]() 的中点为
的中点为![]() ,则
,则![]() 点坐标为
点坐标为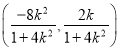
以下分两种情况:
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,线段
,线段![]() 的垂直平分线为
的垂直平分线为![]() 轴,于是
轴,于是
![]()
![]()
![]() 时,线段
时,线段![]() 的垂直平分线方程为
的垂直平分线方程为
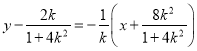 ,令
,令![]() ,解得
,解得![]()
由![]()
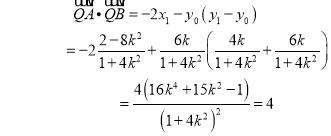
所以: ![]()


科目:高中数学 来源: 题型:
【题目】设f(x)=x2lnx,g(x)=ax3﹣x2 .
(1)求函数f(x)的最小值;
(2)若存在x∈(0,+∞),使f(x)>g(x),求实数a的取值范围;
(3)若使方程f(x)﹣g(x)=0在x∈[ ![]() ,en](其中e=2.7…为自然对数的底数)上有解的最小a的值为an , 数列{an}的前n项和为Sn , 求证:Sn<3.
,en](其中e=2.7…为自然对数的底数)上有解的最小a的值为an , 数列{an}的前n项和为Sn , 求证:Sn<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=n2+2n,(n∈N*),求:
(1)数列{an}的通项公式an;
(2)若bn=an3n , 求数列{bn}的前n项和 Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为一次函数,g(x)为二次函数,且f[g(x)]=g[f(x)].
(1)求f(x)的解析式;
(2)若y=g(x)与x轴及y=f(x)都相切,且g(0)=![]() ,求g(x)的解析式.
,求g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数h(x),其中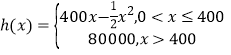 ,x是新样式单车的月产量(单位:件),利润=总收益﹣总成本.
,x是新样式单车的月产量(单位:件),利润=总收益﹣总成本.
(1)试将自行车厂的利润y元表示为月产量x的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com