
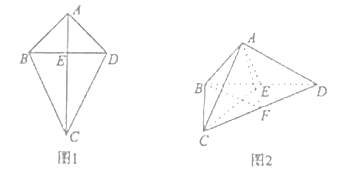
【题目】如图1,四边形![]() 中,
中, ![]() ,
, ![]() ,将四边形
,将四边形![]() 沿着
沿着![]() 折叠,得到图2所示的三棱锥
折叠,得到图2所示的三棱锥![]() ,其中
,其中![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 中点,求二面角
中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析: (1)由面面垂直的判定定理得出证明; (2)以E为原点,建立空间直角坐标系,写出各点坐标,设![]() ,由
,由![]() ,求出
,求出![]() ,求出平面
,求出平面![]() 的一个法向量,由已知条件找出平面
的一个法向量,由已知条件找出平面![]() 的一个法向量,利用公式求出二面角
的一个法向量,利用公式求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)因为![]() 且
且![]() ,可得
,可得![]() 为等腰直角三角形,
为等腰直角三角形,
则![]() ,又
,又![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,
,
故![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)以![]() 为原点,以
为原点,以![]() 的方向为
的方向为![]() 轴正方向,
轴正方向, ![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系.
轴正方向,建立如图所示的空间直角坐标系.

过![]() 点作平面
点作平面![]() 的垂线,垂足为
的垂线,垂足为![]() ,根据对称性,显然
,根据对称性,显然![]() 点在
点在![]() 轴上,设
轴上,设![]() .由题设条件可得下列坐标:
.由题设条件可得下列坐标: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.![]() ,
, ![]() ,由于
,由于![]() ,所以
,所以![]() ,解得
,解得![]() ,则
,则![]() 点坐标为
点坐标为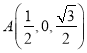 . 由于
. 由于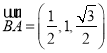 ,
, ![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,
,
由![]() 及
及![]() 得
得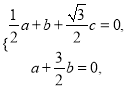
令![]() ,由此可得
,由此可得![]() .
.
由于![]() ,
, ![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则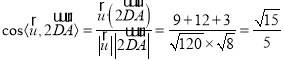 ,
,
因为二面角![]() 为锐角,
为锐角,
则二面角![]() 的余弦值为
的余弦值为![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】“DD共享单车”是为城市人群提供便捷经济、绿色低碳的环保出行方式,根据目前在三明市的投放量与使用的情况,有人作了抽样调查,抽取年龄在二十至五十岁的不同性别的骑行者,统计数据如下表所示:
男性 | 女性 | 合计 | |
20~35岁 |
| 40 | 100 |
36~50岁 | 40 |
| 90 |
合计 | 100 | 90 | 190 |
(1)求统计数据表中![]() 的值;
的值;
(2)假设用抽到的100名20~35岁年龄的骑行者作为样本估计全市的该年龄段男女使用“DD共享单车”情况,现从全市的该年龄段骑行者中随机抽取3人,求恰有一名女性的概率;
(3)根据以上列联表,判断使用“DD共享单车”的人群中,能否有![]() 的把握认为“性别”与“年龄”有关,并说明理由.
的把握认为“性别”与“年龄”有关,并说明理由.
参考数表:
|
|
|
|
|
|
|
|
|
|
参考公式: 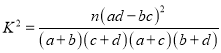 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是两条不重合的直线,
是两条不重合的直线, ![]() 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题:
①若![]() ,
, ![]() ,则
,则![]() ;
;
②若![]() ,
, ![]() ,
, ![]() ,则
,则![]() ;
;
③若![]() ,
, ![]() ,
, ![]() ,则
,则![]() ;
;
④当![]() ,且
,且![]() 时,若
时,若![]() ,则
,则![]() .
.
其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
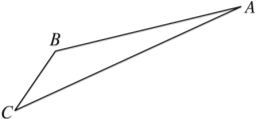
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 到坐标原点的距离和它到直线
到坐标原点的距离和它到直线![]() 的距离之比是一个常数
的距离之比是一个常数![]() .
.
(1)求点![]() 的轨迹;
的轨迹;
(2)若![]() 时得到的曲线是
时得到的曲线是![]() ,将曲线
,将曲线![]() 向左平移一个单位长度后得到曲线
向左平移一个单位长度后得到曲线![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,过
,过![]() 的直线
的直线![]() 分别交曲线
分别交曲线![]() 于点
于点![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于一点
相交于一点![]() ,
, ![]() ,将
,将![]() 沿着
沿着![]() 折起得
折起得![]() ,连接
,连接![]() .
.
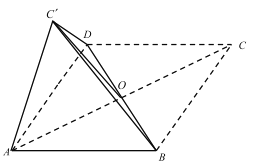
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在平面
在平面![]() 上的投影恰好是
上的投影恰好是![]() 的重心,求直线
的重心,求直线![]() 与底面
与底面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求f(x)的解析式;
(2)若对任意t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人每人有一张游泳比赛的门票,已知每张票可以观看指定的三场比赛中的任一场(三场比赛时间不冲突),甲乙二人约定他们会观看同一场比赛并且他俩观看每场比赛的可能性相同,又已知丙观看每一场比赛的可能性也相同,且甲乙的选择与丙的选择互不影响.
(1)求三人观看同一场比赛的概率;
(2)记观看第一场比赛的人数是![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com