
【题目】已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值.
【答案】解:(Ⅰ)不等式转化为 ![]() 或
或 ![]() ,
,
解得x>2,∴x0=2;
(Ⅱ)由题意,等价于|x﹣m|+|x+ ![]() |=2(m>0)有解,
|=2(m>0)有解,
∵|x﹣m|+|x+ ![]() |≥m+
|≥m+ ![]() ,当且仅当(x﹣m)(x+
,当且仅当(x﹣m)(x+ ![]() )≤0时取等号,
)≤0时取等号,
∵|x﹣m|+|x+ ![]() |=2(m>0)有解,
|=2(m>0)有解,
∴m+ ![]() ≤2,
≤2,
∵m+ ![]() ≥2,
≥2,
∴m+ ![]() =2,∴m=1
=2,∴m=1
【解析】(Ⅰ)不等式转化为 ![]() 或
或 ![]() ,解得x>2,即可求x0的值;(Ⅱ)由题意,等价于|x﹣m|+|x+
,解得x>2,即可求x0的值;(Ⅱ)由题意,等价于|x﹣m|+|x+ ![]() |=2(m>0)有解,结合基本不等式,即可求实数m的值.
|=2(m>0)有解,结合基本不等式,即可求实数m的值.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】已知(x+ ![]() )n展开式的二项式系数之和为256
)n展开式的二项式系数之和为256
(1)求n;
(2)若展开式中常数项为 ![]() ,求m的值;
,求m的值;
(3)若展开式中系数最大项只有第6项和第7项,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,
, ![]() ,点
,点 ![]() 在椭圆上,
在椭圆上, ![]() ,且
,且 ![]() 的面积为4.
的面积为4.
(1)求椭圆的方程;
(2)点 ![]() 是椭圆上任意一点,
是椭圆上任意一点, ![]() 分别是椭圆的左、右顶点,直线
分别是椭圆的左、右顶点,直线 ![]() 与直线
与直线 ![]() 分别交于
分别交于 ![]() 两点,试证:以
两点,试证:以 ![]() 为直径的圆交
为直径的圆交 ![]() 轴于定点,并求该定点的坐标.
轴于定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.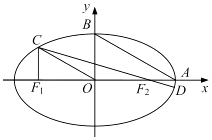
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( ) 
A.2.81
B.2.82
C.2.83
D.2.84
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为1的球O内切于正四面体A﹣BCD,线段MN是球O的一条动直径(M,N是直径的两端点),点P是正四面体A﹣BCD的表面上的一个动点,则 ![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com