
【题目】设函数![]() ,
, ![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,记
时,记![]() 的最小值为
的最小值为![]() ,证明:
,证明: ![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)函数![]() 的定义域为
的定义域为![]() ,对函数
,对函数![]() 求导得
求导得![]() ,对实数
,对实数![]() 分
分![]() 分两种情况讨论,得出单调性;(2)由(1)知,
分两种情况讨论,得出单调性;(2)由(1)知, ![]() ,
, ![]()
![]() ,
, ![]() ,所以
,所以![]() 单调递减,又
单调递减,又![]() ,
, ![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() ,
, ![]() 单调递减;所以
单调递减;所以![]() ,再证明出
,再证明出![]() 。
。
试题解析(1)![]() 的定义域为
的定义域为![]() ,
,
![]()
![]()
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,当
时,当![]() ,
, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() ,
, ![]() ,
, ![]() 单调递增;
单调递增;
综上,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由(1)知, ![]()
![]()
![]() ,
,
即![]() .
.
解法一: ![]()
![]() ,
, ![]() ,
,
∴![]() 单调递减,
单调递减,
又![]() ,
, ![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,
,
∴当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
∴![]()
![]() ,又
,又![]() ,即
,即![]() ,
, ![]() ,
,
∴![]()
![]() ,令
,令![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以
,所以![]() ,∴
,∴![]() .
.
解法二:要证![]() ,即证
,即证![]() ,即证:
,即证: ![]() ,
,
令![]() ,则只需证
,则只需证![]() ,
,
![]()
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
所以![]()
![]() ,
,
所以![]() ,即
,即![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】抢“微信红包”已经成为中国百姓欢度春节时非常喜爱的一项活动.小明收集班内20名同学今年春节期间抢到红包金额![]() (元)如下(四舍五入取整数):
(元)如下(四舍五入取整数):
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
对这20个数据进行分组,各组的频数如下:

(Ⅰ)写出m,n的值,并回答这20名同学抢到的红包金额的中位数落在哪个组别;
(Ⅱ)记C组红包金额的平均数与方差分别为![]() 、
、![]() ,E组红包金额的平均数与方差分别为
,E组红包金额的平均数与方差分别为![]() 、
、![]() ,试分别比较
,试分别比较![]() 与
与![]() 、
、![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从A,E两组所有数据中任取2个,求这2个数据差的绝对值大于100的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() 为棱
为棱![]() 中点.
中点. ![]() ,
, ![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)在棱![]() 的上是否存在点
的上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?如果存在,求此时
?如果存在,求此时![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成![]() 小块地,在总共
小块地,在总共![]() 小块地中.随机选
小块地中.随机选![]() 小块地种植品种甲,另外
小块地种植品种甲,另外![]() 小块地种植品种乙.
小块地种植品种乙.
(![]() )假设
)假设![]() ,求第一大块地都种植品种甲的概率.
,求第一大块地都种植品种甲的概率.
(![]() )试验时每大块地分成
)试验时每大块地分成![]() 小块.即
小块.即![]() ,试验结束后得到品种甲和品种乙在各个小块地上的每公顷产量(单位
,试验结束后得到品种甲和品种乙在各个小块地上的每公顷产量(单位![]() )如下表:
)如下表:
品种甲 |
|
|
|
|
|
品种乙 |
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=Acos(ωx+φ)+B的部分图象如图所示,将函数g(x)的图象保持纵坐标不变,横坐标向右平移![]() 个单位长度后得到函数f(x)的图象.求:
个单位长度后得到函数f(x)的图象.求:
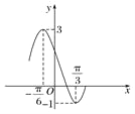
(1)函数f(x)在![]() 上的值域;
上的值域;
(2)使f(x)≥2成立的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
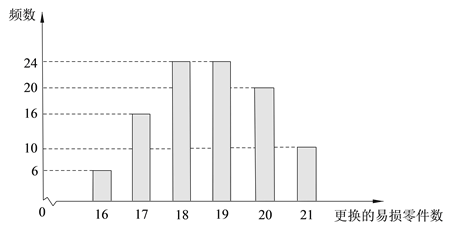
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元), ![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(Ⅰ)若![]() =19,求y与x的函数解析式;
=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于![]() ”的频率不小于0.5,求
”的频率不小于0.5,求![]() 的最小值;
的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com