【题目】大家知道， 莫言是中国首位获得诺贝尔奖的文学家， 国人欢欣鼓舞.某高校文学社从男女生中各抽取
名同学调查对莫言作品的了解程度， 结果如下：
阅读过莫言的作品数（ 篇） |
|
|
|
|
|
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
（1）试估计该校学生阅读莫言作品超过篇的概率；
（2）对莫言作品阅读超过
篇的则称为“对莫言作品非常了解” ， 否则为“ 一般了解” .根据题意完成下表， 并判断能否在犯错误的概率不超过
的前提下， 认为对莫言作品非常了解与性别有关？
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
附：
，其中
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
口算能手系列答案科目：高中数学 来源： 题型：
【题目】某地区2008年至2014年中，每年的居民人均纯收入y（单位：千元）的数据如下表：
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验，得知t与y之间具有线性相关关系．
（1）求y关于t的线性回归方程；
（2）预测该地区2017年的居民人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：
，
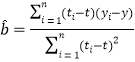查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数y＝loga(x＋3)－1(a＞0，a≠1)的图象恒过定点A.
(1) 求点A的坐标；
(2) 若点A在直线mx＋ny＋1＝0上，其中m，n都是正数，求
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）当
时，求函数
在
上的最大值；
（2）令
，若
在区间
上为单调递增函数，求
的取值范围；
（3）当
时，函数
的图象与
轴交于两点
，且
，又
是
的导函数.若正常数
满足条件
.试比较
与0的关系，并给出理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
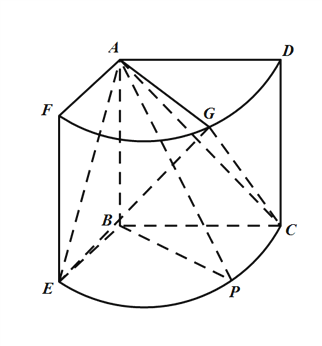
【题目】如图，几何体是圆柱的一部分，它是由矩形
（及其内部）以
边所在直线为旋转轴旋转
得到的， 
是
的中点.
（
）设
是
上的一点，且
，求
的大小;
（
）当
时,求二面角
的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝a－
.
(1)求f(0)；
(2)探究f(x)的单调性，并证明你的结论；
(3)若f(x)为奇函数，求满足f(ax)<f(2)的x的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的两个焦点分别为
，离心率为
.设过点
的直线
与椭圆
相交于不同两点
， 
周长为
.
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知点
，证明：当直线
变化时，总有TA与
的斜率之和为定值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
