
 已知函数
已知函数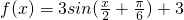
 | 0 |  | π |  | 2 π |
| x | - |  |  | 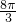 | 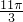 |
| y=3sin(2x+)+3 | 3 | 6 | 3 | 0 | 3 |
 ≤
≤ ≤2kπ+
≤2kπ+ ,k∈z,可得 4kπ-
,k∈z,可得 4kπ- ≤x≤4kπ+
≤x≤4kπ+ ,
, ,4kπ+
,4kπ+ ],k∈z.
],k∈z. 个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),
个单位,再把各点的横坐标变为原来的2倍(纵坐标不变), )+3
)+3 分别等于0,
分别等于0, ,π,
,π, ,2π,求得对应的x,y值,以这五对x,y值作为点的坐标,在坐标系中描出,用平滑曲线连接,即得它在一个周期内的闭区间上的图象.
,2π,求得对应的x,y值,以这五对x,y值作为点的坐标,在坐标系中描出,用平滑曲线连接,即得它在一个周期内的闭区间上的图象. ≤
≤ ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,即得单调增区间.
,k∈z,求得x的范围,即得单调增区间. 个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),再把各点的纵坐标变为原来的3倍(横坐标不变),再把各点向上平移3个单位,即得函数y=3sin(
个单位,再把各点的横坐标变为原来的2倍(纵坐标不变),再把各点的纵坐标变为原来的3倍(横坐标不变),再把各点向上平移3个单位,即得函数y=3sin(  )+3
)+3

科目:高中数学 来源:2015届福建省高一上学期期中考试数学试卷(解析版) 题型:解答题
(10分)已知函数
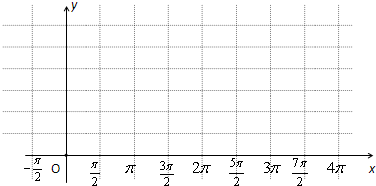
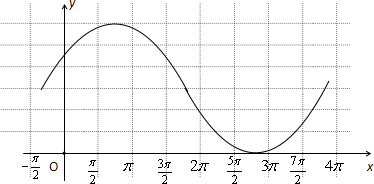
(1)用“五点法”作出这个函数在一个周期内的图象;
(2)函数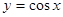 图象经过怎样的变换可以得到
图象经过怎样的变换可以得到 的图象?
的图象?
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古高一下期中考试理科数学卷(二)(解析版) 题型:解答题
已知函数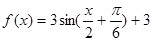
(1)用五点法画出它在一个周期内的闭区间上的图象;
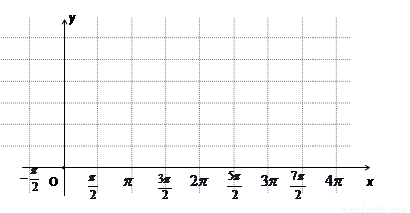
(2)求函数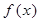 的单调增区间;
的单调增区间;
(3)若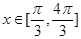 ,求
,求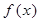 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2014届山东省济南外国语学校高一下期中数学试卷(解析版) 题型:解答题
(满分10分)
已知函数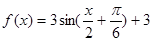
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出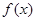 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由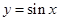 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高一第三阶段检测数学卷 题型:解答题
(本题满分14分)已知函数
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由 上的图象经怎样的变换得到
上的图象经怎样的变换得到
查看答案和解析>>
科目:高中数学 来源:2013届山东省高一下学期期末考试数学 题型:解答题
(本小题满分12分)
已知函数 .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出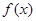 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)写出函数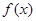 的单调递增区间.
的单调递增区间.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com