练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知， 是两条不同直线， ， 是两个不同平面，则下列命题正确的是（ ）

    A. 若， 垂直于同一平面，则与平行

    B. 若， 平行于同一平面，则与平行

    C. 若， 不平行，则在内不存在与平行的直线

    D. 若， 不平行，则与不可能垂直于同一平面

    【答案】D

    【解析】试题分析：由于α，β垂直于同一平面，则α与β平行，利用正方体的两个相邻侧面不满足题意，故①不对；

    若m，n平行于同一平面，则m与n平行，可能相交也可能平行也可以异面，故②不对；

    若α，β不平行，则在α内不存在与β平行的直线，利用正方体中点侧面与底面，侧面的上底面的棱与下底面的棱，能够找到平行线，所以③不正确；

    若m，n不平行，则m与n不可能垂直于同一平面，如果两条直线垂直同一个平面，则两条直线平行，所以④正确．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某家父母记录了女儿玥玥的年龄（岁）和身高（单位cm）的数据如下：

    年龄x

    6

    7

    8

    9

    身高y

    118

    126

    136

    144


    （1）试求y关于x的线性回归方程 = x+
    （2）试预测玥玥10岁时的身高．（其中， = ， = ﹣ ．

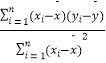    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了普及环保知识，增强环保意识，某校从理科甲班抽取60人，从文科乙班抽取50人参加环保知识测试．

    优秀人数

    非优秀人数

    总计

    甲班

    乙班

    30

    总计

    60

    （Ⅰ）根据题目完成列联表，并据此判断是否有的把握认为环保知识成绩优秀与学生的文理分类有关．

    （Ⅱ）现已知， ， 三人获得优秀的概率分别为， ， ，设随机变量表示， ， 三人中获得优秀的人数，求的分布列及期望．

    附： ，

    0.100

    0.050

    0.025

    0.010

    0.005

    2.706

    3.841

    5.024

    6.635

    7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】山西某公司有一批专业技术人员，对他们进行年龄状况和接受教育程度（本科学历）的调查，其结果（人数分布）如表：

    学历

    35岁以下

    3550岁

    50岁以上

    本科

    80

    30

    20

    研究生

    20

    （Ⅰ）用分层抽样的方法在岁年龄段的专业技术人员中抽取一个容量为10的样本，将该样本看成一个总体，从中任取3人，求至少有1人的学历为研究生的概率；

    （Ⅱ）在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取个人，其中35岁以下48人，50岁以上10人，再从这个人中随机抽取出1人，此人的年龄为50岁以上的概率为，求、的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}是等差数列，且a1=2，a1+a2+a3=12．
    （1）求数列{an}的通项公式；
    （2）令bn=an3n（x∈R）．求数列{bn}前n项和的公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， （为常数）.

    （1）函数的图象在点处的切线与函数的图象相切，求实数的值；

    （2）若函数在定义域上存在单调减区间，求实数的取值范围；

    （3）若， ，且，都有成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn ， 若4Sn=（2n﹣1）an+1+1，且a1=1．
    （1）求数列{an}的通项公式；
    （2）设cn= ，数列{cn}的前n项和为Tn ．
    ①求Tn；
    ②对于任意的n∈N*及x∈R，不等式kx2﹣6kx+k+7+3Tn＞0恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}满足an+1+（﹣1）nan=2n﹣1，则{an}的前60项和为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中，四边形是菱形，,二面角为， .

    （Ⅰ）求证：平面平面;

    （Ⅱ）求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案