
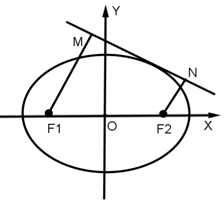
 已知椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$,直线l:y=kx+m与椭圆C有且仅有一个公共点,若F1M⊥l,F2N⊥l,M,N分别为垂足.
已知椭圆C的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$,直线l:y=kx+m与椭圆C有且仅有一个公共点,若F1M⊥l,F2N⊥l,M,N分别为垂足.分析 (Ⅰ)将直线的方程y=kx+m代入椭圆C的方程中,得(4k2+3)x2+8kmx+4m2-12=0.由直线与椭圆C仅有一个公共点知,△=0,化简得:m2=4k2+3.利用点到直线的距离公式可得:d1=|F1M,d2=|F2M|,代入d1d2,化简利用重要不等式的性质即可得出.
(Ⅱ)当k≠0时,设直线的倾斜角为θ,则|d1-d2|=|MN||tanθ|,代入S=$\frac{1}{2}$|MN|•(d1+d2)=$|\frac{{d}_{1}^{2}-{d}_{2}^{2}}{2k}|$=$\frac{2|m|}{{k}^{2}+1}$,由于m2=4k2+3,对k分类讨论,利用基本不等式的性质即可得出.
解答 解:(Ⅰ)证明:将直线的方程y=kx+m代入椭圆C的方程3x2+4y2=12中,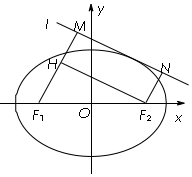
得(4k2+3)x2+8kmx+4m2-12=0.
由直线与椭圆C仅有一个公共点知,
△=64k2m2-4(4k2+3)(4m2-12)=0,
化简得:m2=4k2+3.
设d1=|F1M=$\frac{|-k+m|}{\sqrt{{k}^{2}+1}}$,d2=|F2M|=$\frac{|k+m|}{\sqrt{{k}^{2}+1}}$,
d1d2=$\frac{|-k+m|}{\sqrt{{k}^{2}+1}}$•$\frac{|k+m|}{\sqrt{{k}^{2}+1}}$=$\frac{|{m}^{2}-{k}^{2}|}{{k}^{2}+1}$=$\frac{3{k}^{2}+3}{{k}^{2}+1}$=3,
|F1M|+|F2M|=d1+d2≥$2\sqrt{{d}_{1}{d}_{2}}$=2$\sqrt{3}$.
(Ⅱ)当k≠0时,设直线的倾斜角为θ,
则|d1-d2|=|MN||tanθ|,∴|MN|=$|\frac{{d}_{1}-{d}_{2}}{k}|$,
S=$\frac{1}{2}$|MN|•(d1+d2)=$|\frac{{d}_{1}^{2}-{d}_{2}^{2}}{2k}|$=$\frac{2|m|}{{k}^{2}+1}$=$\frac{2|m|}{\frac{{m}^{2}-3}{4}+1}$=$\frac{8}{|m|+\frac{1}{|m|}}$,
∵m2=4k2+3,∴当k≠0时,|m|$>\sqrt{3}$,
∴$|m|+\frac{1}{|m|}$>$\sqrt{3}$+$\frac{1}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$,
∴S$<2\sqrt{3}$.
当k=0时,四边形F1MNF2是矩形,$S=2\sqrt{3}$.
所以四边形F1MNF2面积S的最大值为2$\sqrt{3}$.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题、点到直线的距离公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单位 | A1 | A2 | A3 | A4 | A5 |
| 平均身高x(单位:cm) | 170 | 174 | 176 | 181 | 179 |
| 平均得分y | 62 | 64 | 66 | 70 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com