
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
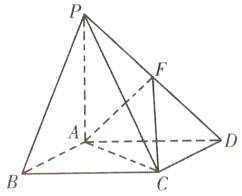
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
【答案】(1)存在,G是线段AB的中点,证明见解析;(2)详见解析
【解析】
(1)设PC的中点为H,连结FH,由题意得AGHF为平行四边形,则AF∥GH,由此能证明在线段AB上存在中点G,使得AF∥平面PCG.
(2)选择①AB⊥BC,推导出AB,AD,AP彼此两两垂直,以AB,AD,AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.选择②FC与平面ABCD所成的角为![]() ,取BC中点E,连结AE,取AD的中点M,连结FM,CM,则FM∥PA,且FM=1,FM⊥平面ABCD,FC与平面ABCD所成角为∠FCM,
,取BC中点E,连结AE,取AD的中点M,连结FM,CM,则FM∥PA,且FM=1,FM⊥平面ABCD,FC与平面ABCD所成角为∠FCM,![]() ,推导出AE,AD,AP彼此两两垂直,以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.选择③∠ABC
,推导出AE,AD,AP彼此两两垂直,以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.选择③∠ABC![]() ,推导出PA⊥BC,取BC中点E,连结AE,推导出 AE,AD,AP彼此两两垂直,以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.
,推导出PA⊥BC,取BC中点E,连结AE,推导出 AE,AD,AP彼此两两垂直,以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.
(1)在线段AB上存在中点G,使得AF∥平面PCG.
证明如下:如图所示:
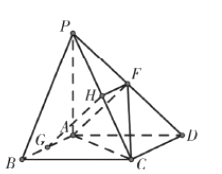
设PC的中点为H,连结FH,
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]()
所以四边形AGHF为平行四边形,
则AF∥GH,
又GH平面PGC,AF平面PGC,
∴AF∥平面PGC.
(2)选择①AB⊥BC:
∵PA⊥平面ABCD,∴PA⊥BC,
由题意知AB,AD,AP彼此两两垂直,
以AB,AD,AP分别为x,y,z轴,建立空间直角坐标系,
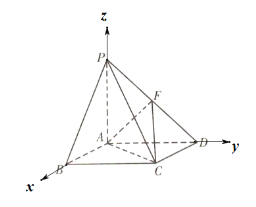
∵PA=AB=2,
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (﹣2,﹣1,1),
(﹣2,﹣1,1),
设平面FAC的一个法向量为![]() (x,y,z),
(x,y,z),
∴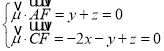 ,
,
取y=1,得![]() (﹣1,1,﹣1),
(﹣1,1,﹣1),
平面ACD的一个法向量为![]() (0,0,1),
(0,0,1),
设二面角F﹣AC﹣D的平面角为θ,
则cosθ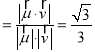 ,
,
∴二面角F﹣AC﹣D的余弦值为![]() .
.
选择②FC与平面ABCD所成的角为![]() :
:
∵PA⊥平面ABCD,取BC中点E,连结AE,取AD的中点M,连结FM,CM,
则FM∥PA,且FM=1,
∴FM⊥平面ABCD,
FC与平面ABCD所成角为∠FCM,∴![]() ,
,
在Rt△FCM中,CM![]() ,
,
又CM=AE,∴AE2+BE2=AB2,∴BC⊥AE,
∴AE,AD,AP彼此两两垂直,
以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,
∵PA=AB=2,
∴A( 0,0,0),B( ![]() ,﹣1,0),C(
,﹣1,0),C(![]() ,1,0),D(0,2,0),E(
,1,0),D(0,2,0),E(![]() ,0,0),F(0,1,1),P(0,0,2),
,0,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (
(![]() ,0,1),
,0,1),
设平面EAC的一个法向量为![]() (x,y,z),
(x,y,z),
则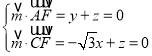 ,
,
取x![]() ,得
,得![]() (
(![]() ,﹣3,3),
,﹣3,3),
平面ACD的一个法向量为:![]() (0,0,1),
(0,0,1),
设二面角F﹣AC﹣D的平面角为θ,
则cosθ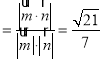 .
.
∴二面角F﹣AC﹣D的余弦值为![]() .
.
选择③∠ABC![]() :
:
∵PA⊥平面ABCD,
∴PA⊥BC,取BC中点E,连结AE,
∵底面ABCD是菱形,∠ABC=60°,∴△ABC是正三角形,
∵E是BC的中点,∴BC⊥AE,
∴AE,AD,AP彼此两两垂直,
以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,
∵PA=AB=2,
∴A( 0,0,0),B( ![]() ,﹣1,0),C(
,﹣1,0),C(![]() ,1,0),D(0,2,0),E(
,1,0),D(0,2,0),E(![]() ,0,0),F(0,1,1),P(0,0,2),
,0,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (
(![]() ,0,1),
,0,1),
设平面EAC的一个法向量为![]() (x,y,z),
(x,y,z),
则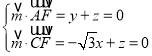 ,
,
取x![]() ,得
,得![]() (
(![]() ,﹣3,3),
,﹣3,3),
平面ACD的法向量![]() (0,0,1),
(0,0,1),
设二面角F﹣AC﹣D的平面角为θ,
θ则cosθ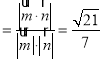 .
.
∴二面角F﹣AC﹣D的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某同学计划用他姓名的首字母![]() ,身份证的后4位数字(4位数字都不同)以及3个符号
,身份证的后4位数字(4位数字都不同)以及3个符号![]() 设置一个六位的密码.若
设置一个六位的密码.若![]() 必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
A.864B.1009C.1225D.1441
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的归家之一,某市为了制订合理的节水方案,对家庭用水情况进行了抽样调查,获得了某年100个家庭的月均用水量(单位:![]() )的数据,将这些数据按照
)的数据,将这些数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
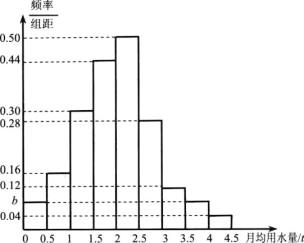
(1)求图中的![]() 值,若该市有30万个家庭,试估计全市月均用水量不低于
值,若该市有30万个家庭,试估计全市月均用水量不低于![]() 的家庭数;
的家庭数;
(2)假设同组中的每个数据都用该组区间的中点值代替,试估计全市家庭月均用水量的平均数;
(3)现从月均用水量在![]() ,
,![]() 的家庭中,先按照分层抽样的方法抽取9个家庭,再从这9家庭中抽取4个家庭,记这4个家庭中月均用水量在
的家庭中,先按照分层抽样的方法抽取9个家庭,再从这9家庭中抽取4个家庭,记这4个家庭中月均用水量在![]() 中的数量为
中的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
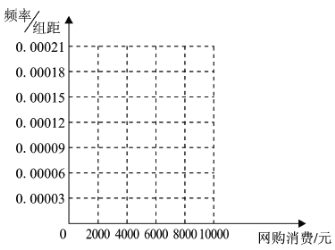
【题目】我国新型冠状病毒肺炎疫情期间,以网络购物和网上服务所代表的新兴消费展现出了强大的生命力,新兴消费将成为我国消费增长的新动能.某市为了了解本地居民在2020年2月至3月两个月网络购物消费情况,在网上随机对1000人做了问卷调查,得如下频数分布表:
网购消费情况(元) |
|
|
|
|
|
频数 | 300 | 400 | 180 | 60 | 60 |
(1)作出这些数据的频率分布直方图,并估计本市居民此期间网络购物的消费平均值;
(2)在调查问卷中有一项是填写本人年龄,为研究网购金额和网购人年龄的关系,以网购金额是否超过4000元为标准进行分层抽样,从上述1000人中抽取200人,得到如下列联表,请将表补充完整并根据列联表判断,在此期间是否有95%的把握认为网购金额与网购人年龄有关.
网购不超过4000元 | 网购超过4000元 | 总计 | |
40岁以上 | 75 | 100 | |
40岁以下(含40岁) | |||
总计 | 200 |
参考公式和数据:![]() .(其中
.(其中![]() 为样本容量)
为样本容量)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
则x∈[﹣1,e]时,f(x)的最小值为_____;设g(x)=[f(x)]2﹣f(x)+a若函数g(x)有6个零点,则实数a的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,极点为![]() ,一条封闭的曲线
,一条封闭的曲线![]() 由四段曲线组成:
由四段曲线组成:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求该封闭曲线所围成的图形面积;
(2)若直线![]() :
:![]() 与曲线
与曲线![]() 恰有3个公共点,求
恰有3个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )
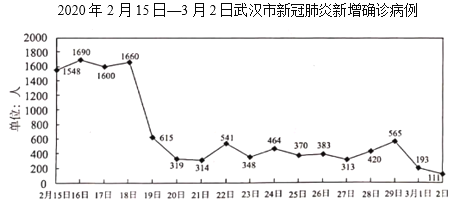
A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com