
【题目】已知函数![]() 是
是![]() 上的偶函数,对于任意
上的偶函数,对于任意![]() 都有
都有![]() 成立,当
成立,当![]() ,且
,且![]() 时,都有
时,都有![]() .给出以下三个命题:
.给出以下三个命题:
①直线![]() 是函数
是函数![]() 图像的一条对称轴;
图像的一条对称轴;
②函数![]() 在区间
在区间![]() 上为增函数;
上为增函数;
③函数![]() 在区间
在区间![]() 上有五个零点.
上有五个零点.
问:以上命题中正确的个数有( ).
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
科目:高中数学 来源: 题型:
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 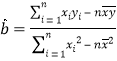 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位拟从40名员工中选1人赠送电影票,可采用下面两种选法:
选法一:将这40名员工按1~40进行编号,并相应地制作号码为140的40个号签,把这40个号签放在一个暗箱中搅匀,最后随机地从中抽取1个号签,与这个号签编号一致的员工幸运入选;
选法二:将39个白球与1个红球(球除颜色外,其他完全相同)混合放在一个暗箱中搅匀,让40名员工逐一从中摸取一个球,则摸到红球的员工幸运入选.试问:
(1)这两种选法是否都是抽签法,为什么?
(2)这两种选法中每名员工被选中的可能性是否相等?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校计划面向高二年级文科学生开设社会科学类和自然退坡在校本选修课程,某文科班有50名学生,对该班选课情况进行统计可知:女生占班级人数的60%,选社会科学类的人数占班级人数的70%,男生有10人选自然科学类.
(1)根据题意完成以下![]() 列联表:
列联表:
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 |
(2)判断是否有99%的把握认为科类的选择与性别有关?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附: ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com