
【题目】假设某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求:(1)y与x之间的回归方程;
(2)当使用年限为10年时,估计维修费用是多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】x,y 满足约束条件  ,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
,若 z=y﹣ax 取得最大值的最优解不唯一,则实数 a 的值为( )
A.![]() 或﹣1
或﹣1
B.2 或 ![]()
C.2 或1
D.2 或﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A是单位圆O和x轴正半轴的交点,P,Q是圆O上两点,O为坐标原点,∠AOP= ![]() ,∠AOQ=α,α∈[0,
,∠AOQ=α,α∈[0, ![]() ].
]. 
(1)若Q( ![]() ,
, ![]() ),求cos(α﹣
),求cos(α﹣ ![]() )的值;
)的值;
(2)设函数f(α)=sinα( ![]()
![]() ),求f(α)的值域.
),求f(α)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产一种产品的固定成本(即固定投入)为0.5万元,但每生产一百件这样的产品,需要增加可变成本(即另增加投入)0.25万元. 市场对此产品的年需求量为500件,销售的收入函数为![]() =
=![]() (单位:万元),其中
(单位:万元),其中![]() 是产品售出的数量(单位:百件).
是产品售出的数量(单位:百件).
(1)该公司这种产品的年产量为![]() 百件,生产并销售这种产品所得到的利润为当年产量
百件,生产并销售这种产品所得到的利润为当年产量![]() 的函数
的函数![]() ,求
,求![]() ;
;
(2)当年产量是多少时,工厂所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SB⊥底面ABC,且SB=AB=2,BC= ![]() ,D、E分别是SA、SC的中点.
,D、E分别是SA、SC的中点. 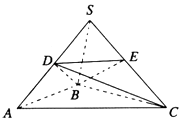
(Ⅰ)求证:平面ACD⊥平面BCD;
(Ⅱ)求二面角S﹣BD﹣E的平面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校,在课堂上,李老师请学生画出自行车行进路程s(千米)与行进时间x(秒)的函数图象的示意图,你认为正确的是
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是A1B1的中点. 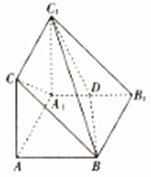
(1)求证:A1C∥平面BDC1;
(2)若AB⊥AC,且AB=AC= ![]() AA1 , 求二面角A﹣BD﹣C1的余弦值.
AA1 , 求二面角A﹣BD﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在非负实数![]() 、
、![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 、
、![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com