
【题目】已知各项均不相等的等差数列{an}的前n项和为Sn,若S3=15,且a3+1为a1+1和a7+1的等比中项.
(1)求数列{an}的通项公式与前n项和Sn;
(2)设Tn为数列{![]() }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[![]() +
+![]() ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由.
【答案】(1)an=2n+1 Sn=n(n+2)
(2)数m=![]() ,见解析
,见解析
【解析】解:(1)设数列{an}的公差为d,由已知,可得
S3=a1+a2+a3=15,得a2=a1+d=5,
由a3+1为a1+1和a7+1的等比中项,
可得(6+d)2=(6-d)×(6+5d),化简得d2-2d=0,
解得d=0(不合题意,舍去)或d=2,
当d=2时,a1=3,其通项公式为an=3+(n-1)×2=2n+1,前n项和Sn=n(n+2).
(2)由(1)知数列{an}的前n项和为Sn=n(n+2),
则有![]() =
=![]() =
=![]() (
(![]() -
-![]() ),
),
Tn=![]() (1-
(1-![]() +
+![]() -
-![]() +
+![]() -
-![]() +…+
+…+![]() -
-![]() +
+![]() -
-![]() )=
)=![]() (1+
(1+![]() -
-![]() -
-![]() )=
)=![]() [
[![]() +
+![]() ].
].
故存在常数m=![]() ,使得Tn=m[
,使得Tn=m[![]() +
+![]() ]成立.
]成立.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
【题目】以下给出了4个命题:
(1)两个长度相等的向量一定相等;
(2)相等的向量起点必相同;
(3)若![]() ,且
,且![]() ,则
,则![]() ;
;
(4)若向量![]() 的模小于
的模小于![]() 的模,则
的模,则![]() .
.
其中正确命题的个数共有( )
A.3 个B.2 个C.1 个D.0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子商务公司随机抽取1000名网购者进行调查.这1000名购物者2018年网购金额(单位:万元)均在区间![]() 内,样本分组为:
内,样本分组为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,购物金额的频率分布直方图如下:
,购物金额的频率分布直方图如下:
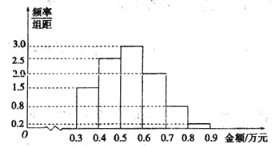
电子商务公司决定给购物者发放优惠券,其金额(单位:元)与购物金额关系如下:
购物金额分组 |
|
|
|
|
发放金额 | 50 | 100 | 150 | 200 |
(1)求这1000名购物者获得优惠券金额的平均数;
(2)以这1000名购物者购物金额落在相应区间的频率作为概率,求一个购物者获得优惠券金额不少于150元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 是参数),
是参数),
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 任一点为
任一点为![]() ,求点
,求点![]() 直线
直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中有大小相同的4个红球和2个白球,给出下列结论:①从中任取3球,恰有一个白球的概率是![]() ;②从中有放回的取球6次,每次任取一球,恰好有两次白球的概率为
;②从中有放回的取球6次,每次任取一球,恰好有两次白球的概率为![]() ;③现从中不放回的取球2次,每次任取1球,则在第一次取到红球后,第二次再次取到红球的概率为
;③现从中不放回的取球2次,每次任取1球,则在第一次取到红球后,第二次再次取到红球的概率为![]() ;④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为
;④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为![]() . 则其中正确命题的序号是( )
. 则其中正确命题的序号是( )
A.①B.②C.③D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]()
(1)求![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)把![]() 的图像上的所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图像向左平移
的图像上的所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图像向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图像,求
的图像,求![]() 的单调减区间
的单调减区间
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,直线
是正方形,直线![]() 平面
平面![]() ,且
,且![]() .
.

(1)求二面角![]() 的大小;
的大小;
(2)设E为棱![]() 的中点,在
的中点,在![]() 的内部或边上是否存在一点
的内部或边上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com