
【题目】在直角坐标系xOy中,直线l过点M(3,4),其倾斜角为45°,圆C的参数方程为 ![]() .再以原点为极点,以x正半轴为极轴建立极坐标系,并使得它与直角坐标系xoy有相同的长度单位.
.再以原点为极点,以x正半轴为极轴建立极坐标系,并使得它与直角坐标系xoy有相同的长度单位.
(1)求圆C的极坐标方程;
(2)设圆C与直线l交于点A、B,求|MA||MB|的值.
【答案】
(1)解:消去参数可得圆的直角坐标方程式为x2+(y﹣2)2=4,
由极坐标与直角坐标互化公式得(ρcosθ)2+(ρsinθ﹣2)2=4化简得ρ=4sinθ
(2)解:直线l的参数方程 ![]() ,(t为参数).
,(t为参数).
即 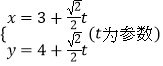 代入圆方程得:
代入圆方程得: ![]() +9=0,
+9=0,
设A、B对应的参数分别为t1、t2,则 ![]() ,t1t2=9,
,t1t2=9,
于是|MA||MB|=|t1||t2|=|t1t2|=9
【解析】(1)利用cos2θ+sin2θ=1消去参数可得圆的直角坐标方程式,由极坐标与直角坐标互化公式代入化简即可得出.(2)直线l的参数方程 ![]() ,(t为参数),代入圆方程得:
,(t为参数),代入圆方程得: ![]() +9=0,利用|MA||MB|=|t1||t2|=|t1t2|即可得出.
+9=0,利用|MA||MB|=|t1||t2|=|t1t2|即可得出.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出v的值为( ) 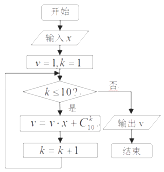
A.210﹣1
B.210
C.310﹣1
D.310
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在研究学习中,收集到某制药厂今年5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
| 1 | 2 | 3 | 4 | 5 |
| 5 | 5 | 6 | 6 | 8 |
若![]() 线性相关,线性回归方程为
线性相关,线性回归方程为![]() ,则以下为真命题的是( )
,则以下为真命题的是( )
A. ![]() 每增加1个单位长度,则
每增加1个单位长度,则![]() 一定增加0.7个单位长度
一定增加0.7个单位长度
B. ![]() 每增加1个单位长度,则
每增加1个单位长度,则![]() 必减少0.7个单位长度
必减少0.7个单位长度
C. 当![]() 时,
时,![]() 的预测值为8.1万盒
的预测值为8.1万盒
D. 线性回归直线![]() 经过点
经过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
分组(重量) |
|
|
|
|
频数(个) | 5 | 10 | 20 | 15 |
(1) 根据频数分布表计算苹果的重量在![]() 的频率;
的频率;
(2) 用分层抽样的方法从重量在![]() 和
和![]() 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在![]() 的有几个?
的有几个?
(3) 在(2)中抽出的4个苹果中,任取2个,求重量在![]() 和
和![]() 中各有1个的概率.
中各有1个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是各项均为正整数的等差数列,公差d∈N* , 且{an}中任意两项之和也是该数列中的一项.
(1)若a1=4,则d的取值集合为;
(2)若a1=2m(m∈N*),则d的所有可能取值的和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知递减等差数列{an}满足:a1=2,a2a3=40. (Ⅰ)求数列{an}的通项公式及前n项和Sn;
(Ⅱ)若递减等比数列{bn}满足:b2=a2 , b4=a4 , 求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=92n﹣1 , n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=nan , 数列{bn}的前n项和为Sn , 若不等式Sn>kan﹣1对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com