练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．从某实验班45名同学中随机抽取5名同学参加“挑战杯”竞赛，用随机数法确定这5名同学，现将随机数表摘录部分如下：
    1622779439495443548217379323788735209643
    8442175331572455068877047447672176335025
    从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字，则选出的第5个同学的编号为（　　）
    A．23B．37C．35D．17

    分析 随机数表法也是简单随机抽样的一种方法，采用随机数表法读数时可以从左向右，也可以从右向左或者从上向下等等．应该注意的是，在读数中出现的相同数据只取一次，超过编号的数据要剔除．

    解答 解：随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字，
    第一个数为39，然后是43，17，37，23，
    故选出来的第5个同学的编号是23，
    故选：A．

    点评 本题主要考查抽样方法，随机数表的使用，考生不要忽略．在随机数表中每个数出现在每个位置的概率是一样的，所以每个数被抽到的概率是一样的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．m，n是空间两条不同直线，α，β是两个不同平面，下面有四个命题：
    ①m⊥α，n∥β，α∥β⇒m⊥n
    ②m⊥n，α∥β，m⊥α⇒n∥β
    ③m⊥n，α∥β，m∥α⇒n⊥β
    ④m⊥α，m∥n，α∥β⇒n⊥β
    其中真命题的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

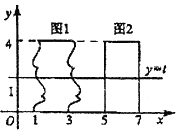    15．我国南北朝时代的数学家祖暅提出体积的计算原理（组暅原理）：“幂势既同，则积不容异”．“势”即是高，“幂”是面积．意思是：如果两等高的几何体在同高处裁得两几何体的裁面积恒等，那么这两个几何体的体积相等，类比祖暅原理，如图所示，在平面直角坐标系中，图1是一个形状不规则的封闭图形，图2是一个矩形，且当实数t取[0，4]上的任意值时，直线y=t被图1和图2所截得的线段始终相等，则图1的面积为8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．一次考试中，5名学生的数学、物理成绩如下：
    学生A1A2A3A4A5
    数学x（分）8991939597
    物理y（分）8789899293
    求y关于x的线性回归方程．
    附：回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．为了了解某校学生喜欢吃辣是否与性别有关，随机对此校100人进行调查，得到如下的列表：
    喜欢吃辣不喜欢吃辣合计
    男生40                  1050                           
    女生2030                      50
    合计6040100
    已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$．
    p（K2≥k）0.100.050.0250.0100.0050.001
    k2.7063.8415.0246.6357.87910.828
    （1）请将上面的列表补充完整；
    （2）是否有99.9%以上的把握认为喜欢吃辣与性别有关？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知α，β都是锐角，sinα=$\frac{4}{5}$，cosβ=$\frac{5}{13}$，则sin（β-α）=（　　）
    A．-$\frac{16}{65}$B．$\frac{16}{65}$C．-$\frac{56}{65}$D．$\frac{56}{65}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．先后抛掷一枚硬币，出现“一次正面，一次反面”的概率为（　　）
    A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{1}{4}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知圆M的方程为x2+（y-2）2=1，直线l的方程为x-2y=0，点P在直线l上，过P点作圆M的切线PA、PB，切点为A、B．
    （1）若点P的坐标为（0，0），求∠APB；
    （2）若点P的坐标为（2，1），过P作直线与圆M交于C、D两点，当$CD=\sqrt{2}$时，求直线CD的方程；
    （3）经过A、P、M三点的圆是否经过异于点M的定点，若经过，请求出此定点的坐标；若不经过，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数$f（x）=2{sin^2}（x+\frac{3π}{2}）+\sqrt{3}$sin（π-2x）
    （1）若$x∈[0，\frac{π}{2}]$，求f（x）的取值范围；
    （2）求函数$y={log_{\frac{1}{2}}}$f（x）的单调增区间．

    查看答案和解析>>

    同步练习册答案