
【题目】求具有下述性质的所有正整数![]() :对任意正整数
:对任意正整数![]() ,
,![]() .
.
【答案】所求的![]() 为
为![]() .
.
【解析】
对正整数![]() ,设
,设![]() 为正整数
为正整数![]() 的标准分解中素因子2的方幂.则
的标准分解中素因子2的方幂.则![]() ,
,
其中![]() 表示正整数
表示正整数![]() 在二进制表示下的数码之和,原命题等价于求所有正整数
在二进制表示下的数码之和,原命题等价于求所有正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,有
,有![]() .再证明所有符号条件的
.再证明所有符号条件的![]() 为
为![]() .
.
对正整数![]() ,设
,设![]() 为正整数
为正整数![]() 的标准分解中素因子2的方幂.则
的标准分解中素因子2的方幂.则
![]() , ①
, ①
其中,![]() 表示正整数
表示正整数![]() 在二进制表示下的数码之和.
在二进制表示下的数码之和.
由![]()
![]() .
.
进而,由式①知本题等价于求所有正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,有
,有![]() .
.
接下来证明:所有符号条件的![]() 为
为.
一方面,因为对任意正整数![]() ,有
,有![]() ,所以,
,所以,![]() 符合条件.
符合条件.
另一方面,若![]() 不为2的方幂,设
不为2的方幂,设![]() (
(![]() ,
,![]() 为大于1的奇数).
为大于1的奇数).
下面构造一个正整数![]() ,使得
,使得![]() .
.
因为![]() ,所以,问题等价于选取
,所以,问题等价于选取![]() 的一个倍数
的一个倍数![]() ,使得
,使得![]() .
.
由![]() ,知存在正整数
,知存在正整数![]() ,使得
,使得![]() .
.
事实上,由欧拉定理,知![]() 可以取
可以取![]() .
.
设奇数![]() 的二进制表示为
的二进制表示为![]() ,其中,
,其中,![]() ,
,![]() .
.
取![]() .
.
则![]() ,且
,且![]() .
.
故![]()
![]()
![]() . ②
. ②
由于![]() ,故正整数
,故正整数![]() 的二进制表示中的最高次幂小于
的二进制表示中的最高次幂小于![]() .
.
由此,对任意整数![]() 、
、![]() ,数
,数![]() 与
与![]() 的二进制表示中没有相同的项.
的二进制表示中没有相同的项.
又![]() ,则
,则![]() 的二进制表示中均不包含1.
的二进制表示中均不包含1.
故由式②知
![]() .
.
因此,上述选取的![]() 满足要求.
满足要求.
综上,所求的![]() 为
为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() 在双曲线
在双曲线![]()
![]() (
(![]() ,
,![]() )上,且双曲线的一条渐近线的方程是
)上,且双曲线的一条渐近线的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 有两个不同的交点,求实数
有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(3)设(2)中直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两个不同的点,若以线段
两个不同的点,若以线段![]() 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲,若点
处成功拦截机器人甲,若点![]() 在矩形区城
在矩形区城![]() 内(包含边界),则挑战成功,否则挑战失败,已知
内(包含边界),则挑战成功,否则挑战失败,已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线远动方式行进.
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线远动方式行进.
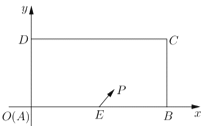
(1)如图建系,求![]() 的轨迹方程;
的轨迹方程;
(2)记![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() ,如何设计
,如何设计![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使之挑战成功?
的值为多少,总可以通过设置机器人乙的释放角度使之挑战成功?
(3)若![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度,才能挑战成功?
足够长,则如何设置机器人乙的释放角度,才能挑战成功?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是一个菱形,三角形PAD是一个等腰三角形,∠BAD=∠PAD=![]() ,点E在线段PC上,且PE=3EC.
,点E在线段PC上,且PE=3EC.
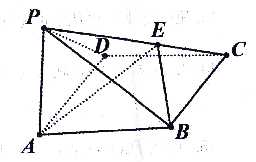
(1)求证:AD⊥PB;
(2)若平面PAD⊥平面ABCD,求二面角E﹣AB﹣P的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com