
【题目】如图1,已知直角梯形ABCD中,![]() ,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
(Ⅰ)求证:平面PAE⊥平面ABCE;
(Ⅱ)求点B到平面PCE的距离.

【答案】(1)见解析(2)![]()
【解析】试题分析:![]() 取
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,可知
,可知![]() ,
,![]() 为等腰直角三角形,证得
为等腰直角三角形,证得![]() ,
,![]() ,再由勾股定理证得
,再由勾股定理证得![]() ,即可证明
,即可证明 ![]() 利用等体积法
利用等体积法![]() ,即可求点
,即可求点![]() 到平面
到平面![]() 的距离
的距离
解析:(Ⅰ)如图,取AE的中点O,连接PO,OB,BE.由于在平面图形中,如题图1,连接BD,BE,易知四边形ABED为正方形, ∴在立体图形中,△PAE,△BAE为等腰直角三角形,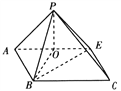
∴PO⊥AE,OB⊥AE,PO=OB=![]() ,
,
∵PB=2,∴![]() ,
,
∴PO⊥OB
又![]() ,∴平面PO⊥平面ABCE,
,∴平面PO⊥平面ABCE,
∵PO![]() 平面PAE,∴平面PAE⊥平面ABCD
平面PAE,∴平面PAE⊥平面ABCD
(Ⅱ)由(Ⅰ)可知,PO⊥AE,OB⊥AE,![]() ,故AE⊥平面POB.
,故AE⊥平面POB.
∵PB![]() 平面POB,∴AE⊥PB,又BC//AE,∴BC⊥PB.
平面POB,∴AE⊥PB,又BC//AE,∴BC⊥PB.
在Rt△PBC中,![]()
在△PEC中,PE=CE=2,
∴![]()
设点B到平面PCE的距离为d,由![]() ,
,
得![]()


科目:高中数学 来源: 题型:
【题目】二进制规定:每个二进制数由若干个0、1组成,且最高位数字必须为1.若在二进制中,![]() 是所有
是所有![]() 位二进制数构成的集合,对于
位二进制数构成的集合,对于![]() ,
,![]() ,
,![]() 表示
表示![]() 和
和![]() 对应位置上数字不同的位置个数.例如当
对应位置上数字不同的位置个数.例如当![]() ,
,![]() 时
时![]() ,当
,当![]() ,
,![]() 时
时![]() .
.
(1)令![]() ,求所有满足
,求所有满足![]() ,且
,且![]() 的
的![]() 的个数;
的个数;
(2)给定![]() ,对于集合
,对于集合![]() 中的所有
中的所有![]() ,求
,求![]() 的和.
的和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)在极坐标系下,设曲线![]() 与射线
与射线![]() 和射线
和射线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的面积;
的面积;
(2)在直角坐标系下,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,且
,且![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 若椭圆![]() 的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点
的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,求椭圆
上,求椭圆![]() 的方程;
的方程;
(2)当![]() 时,若点
时,若点![]() 平分线段
平分线段![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线a与平面![]() 所成角的为30o,直线b在平面
所成角的为30o,直线b在平面![]() 内,且与b异面,若直线a与直线b所成的角为
内,且与b异面,若直线a与直线b所成的角为![]() ,则( )
,则( )
A. 0<![]() ≤30 B. 0<
≤30 B. 0<![]() ≤90 C. 30≤
≤90 C. 30≤![]() ≤90 D. 30≤
≤90 D. 30≤![]() ≤180
≤180
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 为直角梯形,
为直角梯形,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,三棱锥
,三棱锥![]() 的体积为9.
的体积为9.

(1)求![]() 的值;
的值;
(2)过![]() 点的平面
点的平面![]() 平行于平面
平行于平面![]() ,
,![]() 与棱
与棱![]() ,
,![]() ,
,![]() ,
,![]() 分别相交于点
分别相交于点![]() ,求截面
,求截面![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com