
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)当a=1 时,求不等式f(x)≤5的解集;
(2)x0∈R,f(x0)≤|2a+1|,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据绝对值定义将不等式化为三个不等式组,分别求解,最后求并集,(2)先根据绝对值三角不等式得f(x)最小值,再解不等式得a的取值范围.
(1)当a=1时,f(x)=|x﹣1|+|x+2|;
①当x≤﹣2时,f(x)=﹣2x﹣1;
令f(x)≤5,即﹣2x﹣1≤5,解得﹣3≤x≤﹣2;
②当﹣2<x<1时,f(x)=3;
显然f(x)≤5成立,∴﹣2<x<1;
③当x≥1时,f(x)=2x+1;
令f(x)≤5,即2x+1≤5,解得1≤x≤2;
综上所述,不等式的解集为{x|﹣3≤x≤2};
(2)因为f(x)=|x﹣a|+|x+2|≥|(x﹣a)﹣(x+2)|=|a+2|;
又x0∈R,有f(x)≤|2a+1|成立;
所以只需|a+2|≤|2a+1|;
∴(a+2)2≤(2a+1)2;
化简可得a2﹣1≥0,解得a≤﹣1,或a≥1;
∴a的取值范围为(﹣∞,﹣1]∪[1,+∞).


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,t)(t∈R),
=(2cosx,t)(t∈R), ![]() =(sinx﹣cosx,1),函数y=f(x)=
=(sinx﹣cosx,1),函数y=f(x)= ![]()
![]() ,将y=f(x)的图象向左平移
,将y=f(x)的图象向左平移 ![]() 个单位长度后得到y=g(x)的图象且y=g(x)在区间[0,
个单位长度后得到y=g(x)的图象且y=g(x)在区间[0, ![]() ]内的最大值为
]内的最大值为 ![]() .
.
(1)求t的值及y=f(x)的最小正周期;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,若 ![]() g(
g( ![]() ﹣
﹣ ![]() )=﹣1,a=2,求BC边上的高的最大值.
)=﹣1,a=2,求BC边上的高的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试共有10道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有7道题的答案是正确的,其余题中:有一道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.试求出该考生:
(Ⅰ)得50分的概率;
(Ⅱ)所得分数![]() 的数学期望(用小数表示,精确到0.01k^s*5#u)
的数学期望(用小数表示,精确到0.01k^s*5#u)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 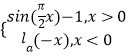 (a>0,且a≠1)的图象上关于y轴对称的点至少有5对,则实数a的取值范围是( )
(a>0,且a≠1)的图象上关于y轴对称的点至少有5对,则实数a的取值范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知圆C的圆心坐标为(2,0),半径为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.,直线l的参数方程为:
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.,直线l的参数方程为: ![]() (t为参数).
(t为参数).
(1)求圆C和直线l的极坐标方程;
(2)点P的极坐标为(1, ![]() ),直线l与圆C相交于A,B,求|PA|+|PB|的值.
),直线l与圆C相交于A,B,求|PA|+|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com