
【题目】已知椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到其两焦点
到其两焦点![]() ,
,![]() 的距离之和为
的距离之和为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且
,且![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
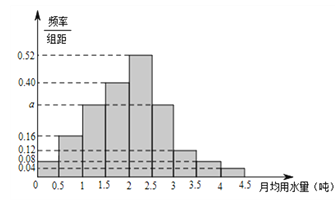
【题目】水是万物之本、生命之源,节约用水,从我做起.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了完成对某城市的工薪阶层是否赞成调整个人所得税税率的调查,随机抽取了60人,作出了他们的月收入频率分布直方图(如图),同时得到了他们月收入情况与赞成人数统计表(如下表):
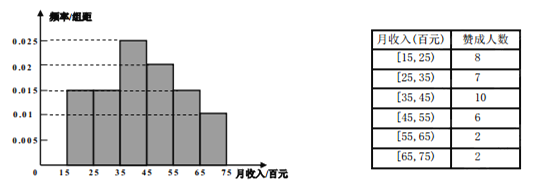
(1)试根据频率分布直方图估计这60人的平均月收入;
(2)若从月收入(单位:百元)在[65,75)的被调查者中随机选取2人进行追踪调查,求2人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远。其中有一题:今有望海岛,立两表齐,高三丈,前后相去千步,令后表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从后表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高及去表各几何? 译文如下:要测量海岛上一座山峰![]() 的高度
的高度![]() ,立两根高均为
,立两根高均为![]() 丈的标杆
丈的标杆![]() 和
和![]() ,前后标杆相距
,前后标杆相距![]() 步,使后标杆杆脚
步,使后标杆杆脚![]() 与前标杆杆脚
与前标杆杆脚![]() 与山峰脚
与山峰脚![]() 在同一直线上,从前标杆杆脚
在同一直线上,从前标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 三点共线,从后标杆杆脚
三点共线,从后标杆杆脚![]() 退行
退行![]() 步到
步到![]() ,人眼著地观测到岛峰,
,人眼著地观测到岛峰,![]() 、
、![]() 、
、![]() 三点也共线,问岛峰的高度
三点也共线,问岛峰的高度![]() 步. (古制:
步. (古制:![]() 步=
步=![]() 尺,
尺,![]() 里=
里=![]() 丈=
丈=![]() 尺=
尺=![]() 步)
步)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】同时抛掷甲、乙两颗骰子.
(1)求事件A“甲的点数大于乙的点数”的概率;
(2)若以抛掷甲、乙两颗骰子点数m,n作为点P的坐标(m,n),求事件B“P落在圆![]() 内”的概率.
内”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 短轴顶点在圆
短轴顶点在圆![]() 上.
上.
(Ⅰ)求椭圆![]() 方程;
方程;
(Ⅱ)已知点![]() ,若斜率为1的直线
,若斜率为1的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究以
两点,试探究以![]() 为底边的等腰三角形
为底边的等腰三角形![]() 是否存在?若存在,求出直线
是否存在?若存在,求出直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
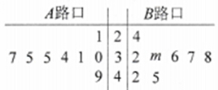
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1) 若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围;
(2) 已知函数f(x)=x2+2mx+3m+4.
① 若函数f(x)有且仅有一个零点,求实数m的值;
若函数f(x)有两个零点且两个零点均比-1大,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com