分析:(1)连A1D、B1C,由正方体性质,AD1⊥A1D,A1B1⊥AD1证出AD1⊥平面A1DCB1,即可证出AD1⊥DM.
(2)在平面A1C1内过点M作MN∥B1C1,交D1C1于N,则∠MCN为CM与平面DC1所成角.在三角形MNC中求出.
(3)由于CC1∥平面D1DMC,将点C到平面D1DM的距离.转化成C1到平面D1DM的距离,作C1H⊥D1M于点H,证出C1H⊥平面D1DM,则C1H为所求距离.
解答: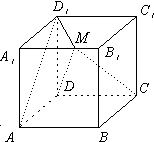
解:(1)证明:连A
1D、B
1C,由正方体性质,AD
1⊥A
1D,A
1B
1⊥AD
1
∴AD1⊥平面A1DCB1
DM?平面A
1DCB
1,∴AD1⊥DM
(2)在平面A
1C
1内过点M作MN∥B
1C
1,交D
1C
1于N,
则MN⊥平面DC
1,连NC.
则∠MCN为CM与平面DC
1所成角 …(6分)
∵MN=B
1C
1=6,MC=
=9
∴sin∠MCN=
=
,即所求正弦值为
.…(8分)
(3)连C
1M,作C
1H⊥D
1M于点H,∵DD
1⊥平面A
1C
1∴D
1D⊥C
1H
∵CC
1∥D
1D
D
1D?平面D
1DM
CC
1?平面D
1DM
∴CC
1∥平面D
1DM
连C
1M,作C
1H⊥D
1M于点H,∵DD
1⊥平面A
1C
1∴D
1D⊥C
1H
∴C
1H⊥平面D
1DM,C
1H为C
1到平面D
1DM的距离即 C到平面D
1DM的距离为C
1H…(10分)
∵
C
1H•D
1M=S
△D1C1M=18,而D
1M=
=
∴C
1H=
∴C到平面D
1DM的距离为
…(12分)
点评:本题主要考查空间角,距离的计算,线面垂直,面面垂直的定义,性质、判定,考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

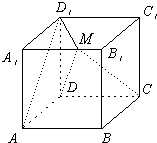 如图,正方体ABCD-A1B1C1D1的棱长为6,动点M在棱A1B1上.
如图,正方体ABCD-A1B1C1D1的棱长为6,动点M在棱A1B1上. 解:(1)证明:连A1D、B1C,由正方体性质,AD1⊥A1D,A1B1⊥AD1
解:(1)证明:连A1D、B1C,由正方体性质,AD1⊥A1D,A1B1⊥AD1

 一本好题口算题卡系列答案
一本好题口算题卡系列答案
 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且BF=DE=C1G=C1H=
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且BF=DE=C1G=C1H=