
【题目】各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N* , 有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn= ![]() ,求数列{bn}的前n项和T.
,求数列{bn}的前n项和T.
【答案】
(1)解:∵a1=1,对任意的n∈N*,有2Sn=2pan2+pan﹣p
∴2a1=2pa12+pa1﹣p,即2=2p+p﹣p,解得p=1
(2)解:2Sn=2an2+an﹣1,①
2Sn﹣1=2an﹣12+an﹣1﹣1,(n≥2),②
①﹣②即得(an﹣an﹣1﹣ ![]() )(an+an﹣1)=0,
)(an+an﹣1)=0,
因为an+an﹣1≠0,所以an﹣an﹣1﹣ ![]() =0,
=0,
∴ ![]()
(3)解:2Sn=2an2+an﹣1=2× ![]() ,
,
∴Sn= ![]() ,
,
∴ ![]() =n2n
=n2n
Tn=1×21+2×22+…+n2n③
又2Tn=1×22+2×23+…+(n﹣1)2n+n2n+1④
④﹣③Tn=﹣1×21﹣(22+23+…+2n)+n2n+1=(n﹣1)2n+1+2
∴Tn=(n﹣1)2n+1+2
【解析】(1)根据a1=1,对任意的n∈N*,有2Sn=2pan2+pan﹣p,令n=1,解方程即可求得结果;(2)由2Sn=2an2+an﹣1,知2Sn﹣1=2an﹣12+an﹣1﹣1,(n≥2),所以(an﹣an﹣1﹣1)(an+an﹣1)=0,由此能求出数列{an}的通项公式.(3)根据 ![]() 求出数列{bn}的通项公式,利用错位相减法即可求得结果.
求出数列{bn}的通项公式,利用错位相减法即可求得结果.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系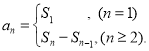 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).


(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:  ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() (t为参数),
(t为参数), ![]() (
( ![]() 为参数).
为参数).
(1)化 ![]() ,
, ![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)过曲线 ![]() 的左顶点且倾斜角为
的左顶点且倾斜角为 ![]() 的直线
的直线 ![]() 交曲线
交曲线 ![]() 于
于 ![]() 两点,求
两点,求 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
(1)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
(2)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注:  ,其中
,其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() :
: 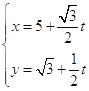 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为 ![]() .
.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为 ![]() ,直线l与曲线C的交点为A,B,求|MA||MB|的值.
,直线l与曲线C的交点为A,B,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() 的离心率为
的离心率为![]() 是
是![]() 和
和![]() 的等比中项.
的等比中项.
(1)求曲线![]() 的方程;
的方程;
(2)倾斜角为![]() 的直线过原点
的直线过原点![]() 且与
且与![]() 交于
交于![]() 两点,倾斜角为
两点,倾斜角为![]() 的直线过
的直线过![]() 且与
且与![]() 交于
交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com