
����Ŀ�������꣬���ڻ�������Ⱦ������Խ��Խ���أ�ij������˾����һ��PM2.5���������������������ӭ����֪���ֿ��ֵĽ���Ϊ40Ԫ�����������в����������y������������۵���x��Ԫ��������ͼ��ʾ��һ�κ�����ϵ��ÿ���������ֿ��ֵ��ܿ�֧z����Ԫ�����������ۣ���������y����������ں�����ϵz=10y+42.5�� 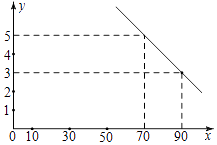
��I����y����x�ĺ�����ϵ��
��II��д���ù�˾�������ֿ��������W����Ԫ���������۵���x��Ԫ���ĺ�����ϵʽ
�������=�������ܽ������ۿ��ֵ��ܽ��۩����ܿ�֧���������۵���xΪ��ֵʱ�����������������Ƕ��٣�
��III������˾ϣ���ÿ���һ������ۻ���������57.5��Ԫ����ù�˾���ֿ��ֵ����۵���Ӧ����ʲô��Χ���ڴ�������Ҫʹ���ֵ��������������Ϊ���۵���Ӧ��Ϊ����Ԫ��
���𰸡��⣺��I�������⣬��y=kx+b��ͼ����㣨70��5������90��3���� ![]() ����k=��
����k=�� ![]() ��b=12��
��b=12��
�� ![]()
��II�� �����⣬��
w=y��x��40����z
=y��x��40������10y+42.5��
=���� ![]() x+12����x��40����10����
x+12����x��40����10���� ![]() x+12����42.5
x+12����42.5
=��0.1x2+17x��642.5=�� ![]() ��x��85��2+80��
��x��85��2+80��
�����۵���Ϊ85Ԫʱ�������������ֵΪ80��Ԫ
��III����W��57.5����0.1x2+17x��642.5��57.5��
������x2��170x+7000��0�����70��x��100��
��Ҫʹ�ÿ���һ������ۻ���������57.5��Ԫ������Ӧ��70Ԫ��100Ԫ֮�䣮
����Ϊ���۵���Խ�ͣ�������Խ������Ҫʹ����������һ���������57.5��Ԫ�����۵���Ӧ��Ϊ70Ԫ��
����������I����ͼ���֪y����x�ĺ�����ϵʽ��һ�κ�������y=kx+b���á����㷨���������ʽ����II�����������=�������ܽ��һ�����۲�Ʒ���ܽ���һ���ܿ�֧���г�������ϵʽ����III����W��57.5���Ӷ�ȷ�����۵���x�ķ�Χ�������κ���w���ʱ��x��ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=�� ![]() ��x��2x ��
��x��2x ��
��1����f��x��= ![]() ����x��ֵ��
����x��ֵ��
��2��������ʽf��2m��mcos�ȣ�+f����1��cos�ȣ���f��0�������Цȡ�[0�� ![]() ]����������ʵ��m��ȡֵ��Χ��
]����������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������C�ϵĶ���M������F��1��0���ľ����������ֱ��x=3�ľ���֮����1�� ![]() ��
��
��1��������C�ķ��̣�
��2������F��1��0����ֱ��l��C����A��B���㣬����ABO���Ϊ ![]() ʱ����ֱ��l�ķ��̣�
ʱ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����C�� ![]() =1����M������C�Ľ��㲻�غϣ�����M��������C����������ĶԳƵ�ֱ�ΪA��B��M��N������ƽ���ڵ����㣬���߶�MN���е�Pǡ����˫����C�ϣ���|AN��BN|= ��
=1����M������C�Ľ��㲻�غϣ�����M��������C����������ĶԳƵ�ֱ�ΪA��B��M��N������ƽ���ڵ����㣬���߶�MN���е�Pǡ����˫����C�ϣ���|AN��BN|= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������� ![]() ����
���� ![]() ����y=|x��1|����y=2x+1 �� ���������䣨0��1���ϵ����ݼ��ĺ�������ǣ� ��
����y=|x��1|����y=2x+1 �� ���������䣨0��1���ϵ����ݼ��ĺ�������ǣ� ��
A.�٢�
B.�ڢ�
C.�ۢ�
D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=Asin����x+�գ���x��R������A��0���أ�0��0���գ� ![]() ����ͼ����x���������������ľ���Ϊ
����ͼ����x���������������ľ���Ϊ ![]() ����ͼ����һ����͵�ΪM��
����ͼ����һ����͵�ΪM�� ![]() ����2���� ������f��x���Ľ���ʽ��
����2���� ������f��x���Ľ���ʽ��
������f��x���ĵ����������䣻
����x��[ ![]() ��
�� ![]() ]ʱ����f��x����ֵ��
]ʱ����f��x����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}�ǹ���d��Ϊ0�ĵȲ����У�a1=2��SnΪ��ǰn��ͣ�
��1����a3=6ʱ����a1 �� a3 �� ![]() ��
�� ![]() ����
���� ![]() �ɵȱ����У�����3��n1��n2������nk������nk�ı���ʽ��
�ɵȱ����У�����3��n1��n2������nk������nk�ı���ʽ��
��2���Ƿ���ں��ʵĹ���d��ʹ��{an}������ǰ3n���У�ǰn��ĺ����n��ĺ͵ı�ֵ���ڶ����������d���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ����P��ABCD������ͼ��ͼ��ʾ��E�Dz���PC�ϵĶ��㣮 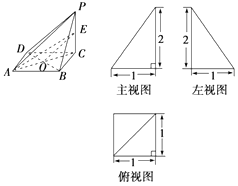
����������P��ABCD�������
��������EΪPC���е㣬AC��BD=O����֤��EO��ƽ��PAD��
�����Ƿ��۵�E�ں�λ�ã�����BD��AE��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com