
已知函数f(x)=2ax- -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0)
(Ⅰ)当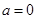 时,求
时,求 的极值;
的极值;
(Ⅱ)当a>0时,讨论 的单调性;
的单调性;
(Ⅲ)若对任意的a∈(2,3),x1,x2∈[1,3],恒有 成立,求实数m的取值范围。
成立,求实数m的取值范围。
(Ⅰ) 的极大值为
的极大值为 ,无极小值;(Ⅱ)①当
,无极小值;(Ⅱ)①当 时,
时, 在
在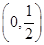 和
和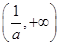 上是增函数,在
上是增函数,在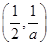 上是减函数;②当
上是减函数;②当 时,
时, 在
在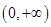 上是增函数;③当
上是增函数;③当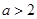 时,
时, 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数 ; (Ⅲ)
上是减函数 ; (Ⅲ)
【解析】
试题分析:(Ⅰ)当 时,求
时,求 的极值,首先确定函数的定义域为
的极值,首先确定函数的定义域为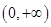 ,对函数
,对函数 求导函数
求导函数 ,确定函数的单调性,即可求得函数
,确定函数的单调性,即可求得函数 的极值;(Ⅱ)当a>0时,讨论
的极值;(Ⅱ)当a>0时,讨论 的单调性,首先对函数
的单调性,首先对函数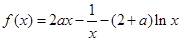 求导函数
求导函数 ,并分解得
,并分解得 ,再进行分类讨论,利用
,再进行分类讨论,利用 ,确定函数单调减区间;
,确定函数单调减区间; ,确定函数的单调增区间;(Ⅲ)若对任意的a∈(2, 3),x1, x2∈[1, 3],恒有
,确定函数的单调增区间;(Ⅲ)若对任意的a∈(2, 3),x1, x2∈[1, 3],恒有 成立,只要求出
成立,只要求出 的最大值即可,因此确定函数
的最大值即可,因此确定函数 在
在 上单调递减,可得
上单调递减,可得 的最大值与最小值,从而得
的最大值与最小值,从而得 ,进而利用分离参数法,可得
,进而利用分离参数法,可得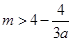 ,从而可求实数
,从而可求实数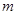 的取值范围
的取值范围
试题解析:(Ⅰ)当 时,
时,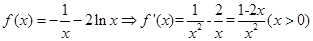 2分
2分
由 ,解得
,解得 ,可知
,可知 在
在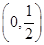 上是增函数,在
上是增函数,在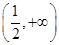 上是减函数 4分
上是减函数 4分
∴ 的极大值为
的极大值为 ,无极小值
5分
,无极小值
5分
(Ⅱ) ,
,
①当 时,
时, 在
在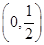 和
和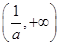 上是增函数,在
上是增函数,在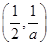 上是减函数; 7分
上是减函数; 7分
②当 时,
时, 在
在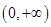 上是增函数;
8分
上是增函数;
8分
③当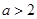 时,
时, 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数 9分
上是减函数 9分
(Ⅲ)当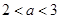 时,由(2)可知
时,由(2)可知 在
在 上是增函数,
上是增函数,
∴ 10分
10分
由 对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
∴ 11分
11分
即 对任意
对任意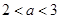 恒成立,
恒成立,
即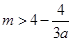 对任意
对任意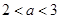 恒成立,
12分
恒成立,
12分
由于当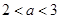 时,
时, ,∴
,∴ 14分
14分
考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性;函数在某点取得极值的条件


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:设计必修一数学北师版 北师版 题型:013
已知函数f(x)=2+log3x(1≤x≤9),则函数y=[f(x)]2+f(x2)的最大值为
A.6
B.13
C.22
D.33
查看答案和解析>>
科目:高中数学 来源:学习高手必修一数学苏教版 苏教版 题型:013
已知函数f(x)=2-x2,g(x)=x.若f(x)·g(x)=min{f(x),g(x)},那么f(x)·g(x)的最大值是
1
2
3
4
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修1) 2009-2010学年 第7期 总163期 人教课标高一版 题型:044
已知函数f(x)=2(log2x)2+2alog2![]() +b,当x=
+b,当x=![]() 时,f(x)有最小值-8,求b的值.
时,f(x)有最小值-8,求b的值.
查看答案和解析>>
科目:高中数学 来源:湖北省孝感高级中学2011-2012学年高一上学期期中考试数学试题 题型:044
已知函数f(x)=2|x|-2.

(1)作出函数f(x)的图象;
(2)由图象指出函数的单调区间及单调性(不用证明);
(3)指出函数的值域.
查看答案和解析>>
科目:高中数学 来源:陕西省宝鸡市2010届高三教学质量检测(二)数学文科试题 题型:013
已知函数f(x)=(![]() )2-log2x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)值的情况是
)2-log2x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)值的情况是
恒为值负
等于0
恒为正值
不大于0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com