
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M、N,若OM=ON,求圆C的方程.
(1)见解析;(2)(x-2)2+(y-1)2=5.
【解析】
试题分析:(1)先求出圆的方程,然后求出与坐标轴的交点坐标,然后求S△AOB=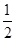 OA·OB=
OA·OB=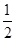 |2t|·
|2t|· =4为定值;(2)由OM=ON,知O在MN的中垂线上,设MN的中点为H,则CH⊥MN,由C、H、O三点共线求出t=2或t=-2,从而得出圆方程.此题注意圆方程的取舍.
=4为定值;(2)由OM=ON,知O在MN的中垂线上,设MN的中点为H,则CH⊥MN,由C、H、O三点共线求出t=2或t=-2,从而得出圆方程.此题注意圆方程的取舍.
试题解析: (1)证明 由题设知,圆C的方程为(x-t)2+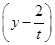 2=t2+
2=t2+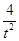 ,
,
化简得x2-2tx+y2-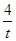 y=0,当y=0时,x=0或2t,则A(2t,0);
y=0,当y=0时,x=0或2t,则A(2t,0);
当x=0时,y=0或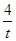 ,则B
,则B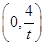 ,∴S△AOB=
,∴S△AOB=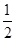 OA·OB=
OA·OB=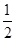 |2t|·
|2t|· =4为定值.
=4为定值.
(2)解 ∵OM=ON,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,
∴C、H、O三点共线,则直线OC的斜率k=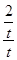 =
=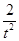 =
=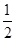 ,∴t=2或t=-2.
,∴t=2或t=-2.
∴圆心为C(2,1)或C(-2,-1).
∴圆C的方程为(x-2)2+(y-1)2=5或(x+2)2+(y+1)2=5,
由于当圆方程为(x+2)2+(y+1)2=5时,直线2x+y-4=0到圆心的距离d>r,此时不满足直线与圆相交,故舍去.
∴圆C的方程为(x-2)2+(y-1)2=5.
考点:1.圆的标准方程;2.直线与圆的位置关系.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:江西省新余一中2011-2012学年高二下学期第一次段考数学理科试题 题型:044
已知以点C(t,![]() )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
(1)求证:△OAB的面积为定值;
(2)设直线y=-2x+4与圆C交于点M,N若|OM|=|ON|,求圆C的方程.
(3)若t>0,当圆C的半径最小时,圆C上至少有三个不同的点到直线l:y-![]() =k(x-3-
=k(x-3-![]() )的距离为
)的距离为![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013届江西省高二下学期第一次段考理科数学试卷 题型:解答题
已知以点C (t,
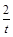 )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
(1)求证:△OAB的面积为定值;
(2)设直线y= –2x+4与圆C交于点M,N若|OM|=|ON|,求圆C的方程.
(3)若t>0,当圆C的半径最小时,圆C上至少有三个不同的点到直线l:y – 的距离为
的距离为 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年湖北省高一下学期期末考试数学试卷 题型:解答题
(本小题12分)已知: 以点C (t, )(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A, 与y轴交于点O, B, 其中O为原点.
轴交于点O, A, 与y轴交于点O, B, 其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N, 若OM = ON, 求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(15分)已知以点C (t, )(t∈R , t ≠ 0)为圆心的圆与![]() 轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com