
 PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ����Ҳ��Ϊ����ο�����ҹ�PM2.5������������֯�趨�������ֵ����PM2.5�վ�ֵ��35��/���������¿�������Ϊһ������35��/������--75��/������֮���������Ϊ��������75��/���������Ͽ�������Ϊ���꣮ij�л����ִ���������9��ÿ���PM2.5��������У���ϵͳ����������ȡ��ij6���������Ϊ����������ֵ�羥Ҷͼ��ʾ��
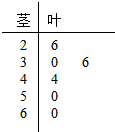
PM2.5��ָ������ֱ��С�ڻ����2.5�Ŀ����Ҳ��Ϊ����ο�����ҹ�PM2.5������������֯�趨�������ֵ����PM2.5�վ�ֵ��35��/���������¿�������Ϊһ������35��/������--75��/������֮���������Ϊ��������75��/���������Ͽ�������Ϊ���꣮ij�л����ִ���������9��ÿ���PM2.5��������У���ϵͳ����������ȡ��ij6���������Ϊ����������ֵ�羥Ҷͼ��ʾ������ ��1�����þ�Ҷͼ������������ݵ�ƽ�����ͷ��
��2���ɾ�Ҷͼ��֪����������6������2���������Ϊһ������4���������Ϊ��������ο���ȡ��ֵΪ1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��м�������
��� �⣺��1��$\overline{x}$=$\frac{1}{6}$����26+30+36+44+50+60��=41
s2=$\frac{1}{6}$��[��26-41��2+��30-41��2+��36-41��2+��44-41��2+��50-41��2+��60-41��2]=137����4�֣�
�����������ƽ���9�·ݸ�����ÿ��PM2.5��ƽ��ֵΪ��41��/�����ף�����Ϊ137������5�֣�
��2���Ӿ�Ҷͼ֪����������6������2���������Ϊһ������4���������Ϊ��������ο���ȡ��ֵΪ1��2��3��
����P����=1��=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$��$P����=2��=\frac{C_4^2•C_2^1}{C_6^3}=\frac{3}{5}$��P����=2��=$\frac{{C}_{4}^{3}{C}_{2}^{0}}{{C}_{6}^{3}}$=$\frac{1}{5}$����10�֣�
��εķֲ���Ϊ
| �� | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���� ���⿼��ƽ�����ͷ������������ɢ����������ķֲ��У�����������ѧ֪ʶ���ʵ�����⣬�����е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x0��1 | B�� | x0��3 | C�� | 2��x0��3 | D�� | 1��x0��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-3��2+y2=25 | B�� | ��x-3��2+y2=16 | C�� | ��x+3��2+y2=16 | D�� | ��x+3��2+y2=25 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{5��}{6}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com