
分析 (1)利用二倍角公式cos2C=1-2sin2C求解即可,注意隐含条件sinC>0;
(2)由sinC=$\frac{3}{4}$,可求cosC,由a=$\frac{\sqrt{2}}{3}$c,又正弦定理可得sinA,cosA,利用两角和的正弦函数公式可求sinB,由正弦定理可得a的值.
解答 解:(1)由已知可得1-2sin2C=-$\frac{1}{8}$.所以sin2C=$\frac{9}{16}$.
因为在△ABC中,sinC>0,
所以sinC=$\frac{3}{4}$.(6分)
(2)∵在锐角△ABC中,sinC=$\frac{3}{4}$,∴可得cosC=$\frac{\sqrt{7}}{4}$,
∵a=$\frac{\sqrt{2}}{3}$c,可得:$\frac{a}{c}=\frac{\sqrt{2}}{3}$,又由正弦定理可得:$\frac{a}{c}=\frac{sinA}{sinC}$,
∴可得:sinA=$\frac{\sqrt{2}}{3}$sinC=$\frac{\sqrt{2}}{3}×\frac{3}{4}$=$\frac{\sqrt{2}}{4}$,解得:cosA=$\frac{\sqrt{14}}{4}$,
∴sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{\sqrt{2}}{4}×\frac{\sqrt{7}}{4}+$$\frac{\sqrt{14}}{4}×\frac{3}{4}$=$\frac{\sqrt{14}}{4}$,
∴由正弦定理可得:a=$\frac{bsinA}{sinB}$=$\frac{3\sqrt{7}×\frac{\sqrt{2}}{4}}{\frac{\sqrt{14}}{4}}$=3.
点评 此类问题是高考的常考题型,主要考查了正弦定理、三角函数及三角恒等变换等知识点,同时考查了学生的基本运算能力和利用三角公式进行恒等变形的技能.


科目:高中数学 来源: 题型:解答题
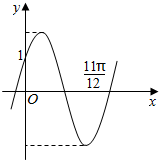 函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示
函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{9}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com