
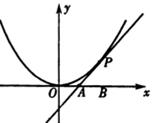
如图,已知直线l与抛物线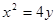 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
(I) 若动点M满足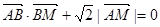 ,求点M的轨迹C;
,求点M的轨迹C;
(II)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围
解:(I)由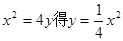 ,
,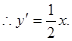 ∴直线l的斜率为
∴直线l的斜率为 ,………1分
,………1分
故l的方程为 ,∴点A坐标为(1,0) ……………………………… 2分
,∴点A坐标为(1,0) ……………………………… 2分
设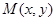 则
则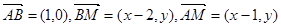 ,
,
由 得
得 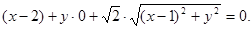
整理,得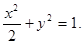 ……………………………………………………4分
……………………………………………………4分
∴点M的轨迹为以原点为中心,焦点在x轴上,长轴长为 ,短轴长为2的椭圆 5分
,短轴长为2的椭圆 5分
(II)如图,由题意知直线l的斜率存在且不为零,设l方程为y=k(x-2)(k≠0)①
将①代入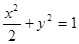 ,整理,得
,整理,得
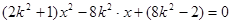 ,
,
由△>0得0<k2< . 设E(x1,y1),F(x2,y2)
. 设E(x1,y1),F(x2,y2)
则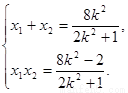 ②
………………………………………………………7分
②
………………………………………………………7分
令 ,由此可得
,由此可得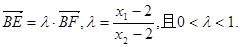
由②知
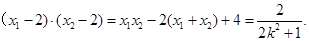
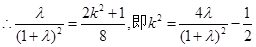 …………………………10分
…………………………10分
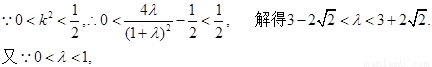
 .
.
∴△OBE与△OBF面积之比的取值范围是(3-2 ,1)…12分.
,1)…12分.
【解析】略


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).| AB |
| BM |
| 2 |
| AM |
| F2E |
| F2F |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知直线l与抛物线y=
如图,已知直线l与抛物线y=| 1 |
| 4 |
| AB |
| BM |
| 2 |
| AM |
| BE |
| BF |
查看答案和解析>>
科目:高中数学 来源: 题型:
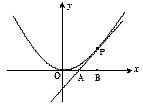 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).| AB |
| BM |
| 2 |
| AM |
查看答案和解析>>
科目:高中数学 来源: 题型:
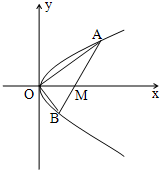 如图,已知直线l与抛物线y2=x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-1,
如图,已知直线l与抛物线y2=x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-1,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com