Question

已知α＝－1910°.

(1)把α写成β＋k·360°(k∈Z,0°≤β<360°)的形式，指出它是第几象限的角；

(2)求θ，使θ与α的终边相同，且－720°≤θ<0°.

 

Answer 1

【答案】

（1）第三象限的角．（2）θ＝－110°或－470°

【解析】在0°到360°的范围里找出与α终边相同的角，可用除以360°求余数的办法来解，也可以考虑把问题转化为求某个不等式的最大整数解问题．解答(1)、(2)的关键都是能正确写出与其角终边相同的角．

解：(1)设α＝β＋k·360°(k∈Z)，则β＝－1910°－k·360°(k∈Z)．令－1910°－k·360°≥0，解得k≤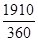－＝－5.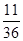

k的最大整数解为k＝－6，求出相应的β＝250°，于是α＝250°－6×360°，它是第三象限的角．

(2)令θ＝250°＋k·360°(k∈Z)，

取k＝－1，－2就得到符合－720°≤θ<0°的角：

250°－360°＝－110°，250°－720°＝－470°.

故θ＝－110°或－470°