
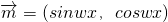 ,
,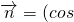 φ,sinφ),函数
φ,sinφ),函数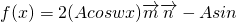 φ (其中
φ (其中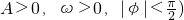 的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为P(
的图象在y轴右侧的第一个最高点(即函数取得最大值的点)为P( ,2),在原点右侧与x轴的第一个交点为Q(
,2),在原点右侧与x轴的第一个交点为Q( ,0).
,0).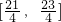 上是否存在对称轴,存在求出方程;否则说明理由.
上是否存在对称轴,存在求出方程;否则说明理由.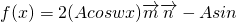 φ=2Acosωx(sinωxcosφ+cosωxsinφ)-Asinφ
φ=2Acosωx(sinωxcosφ+cosωxsinφ)-Asinφ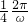 =
=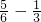 ,∴ω=π.
,∴ω=π. ,2)代入 y=2sin(πx+φ)可得:sin(
,2)代入 y=2sin(πx+φ)可得:sin( +φ)=1,∴φ=2kπ+
+φ)=1,∴φ=2kπ+ ,k∈z.
,k∈z. ,所以
,所以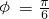 ,于是函数的表达式为 f(x)=2sin(πx+
,于是函数的表达式为 f(x)=2sin(πx+ ). (6分)
). (6分) =kπ+
=kπ+ k∈z,解得x=k+
k∈z,解得x=k+ .
. ≤k+
≤k+ ≤
≤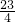 ,解得:
,解得: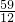 ≤k≤
≤k≤ . 由于k∈z,所以k=5.
. 由于k∈z,所以k=5.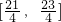 上存在对称轴,其方程为x=
上存在对称轴,其方程为x= . …(10分)
. …(10分) =kπ+
=kπ+ k∈z,解得x=k+
k∈z,解得x=k+ .令
.令  ≤k+
≤k+ ≤
≤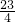 以及k的性质,解得k的值,从而得出结论.
以及k的性质,解得k的值,从而得出结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、π |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•西城区二模)已知函数f(x)=sin(ωx+φ)+
(2012•西城区二模)已知函数f(x)=sin(ωx+φ)+| 3 |
| π |
| 2 |
| π |
| 2 |
| α |
| 4 |
4
| ||
| 5 |
| 2sinα-sin2α |
| 2sinα+sin2α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com