
【题目】已知三棱锥A﹣BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形. 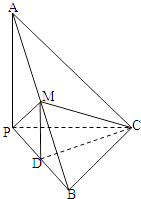
(1)求证:BC⊥平面APC;
(2)若BC=3,AB=10,求三棱锥B﹣MDC的体积VB﹣MDC .
【答案】
(1)证明:∵△PMB为正三角形,
且D为PB的中点,∴MD⊥PB.
又∵M为AB的中点,D为PB的中点,
∴MD∥AP,∴AP⊥PB.
又已知AP⊥PC,∴AP⊥平面PBC,
∴AP⊥BC,又∵AC⊥BC,AC∩AP=A,
∴BC⊥平面APC
(2)解:有VM﹣BCD=VB﹣MDC.
∵AB=10,∴MB=PB=5,
又BC=3,BC⊥PC,∴PC=4,
∴ ![]() .
.
又 ![]() ,∴
,∴ ![]() .
.
【解析】(1)运用等边三角形的性质和中位线定理,证得AP⊥平面PBC,再由线面垂直的性质得,AP⊥BC,结合条件AC⊥BC,即可得证;(2)运用VM﹣BCD=VB﹣MDC . 由棱锥的体积公式,计算三角形BCD的面积和MD,即可得到.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]()
![]() ,且与定直线
,且与定直线![]() 相切,动圆圆心
相切,动圆圆心![]() 的轨迹方程为
的轨迹方程为![]() ,直线
,直线![]() 过点
过点![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)若![]() 交
交![]() 轴于点
轴于点![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 的倾斜角为
的倾斜角为![]() ,在
,在![]() 上是否存在点
上是否存在点![]() 使
使![]() 为正三角形?若能,求点
为正三角形?若能,求点![]() 的坐标;若不能,说明理由.
的坐标;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解湖南各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |
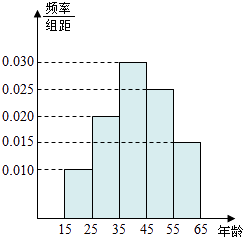
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为ρsin(θ+ ![]() )=
)= ![]() ,圆C的方程为
,圆C的方程为 ![]() (θ为参数).
(θ为参数).
(1)把直线l和圆C的方程化为普通方程;
(2)求圆C上的点到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为4的直角三角形.
是面积为4的直角三角形.
(1)求该椭圆的离心率和标准方程;
(2)过![]() 做直线
做直线![]() 交椭圆于
交椭圆于![]() 两点,使
两点,使![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线
,斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以
两点,以![]() 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2) ![]() 为椭圆
为椭圆![]() 上任意一点,若
上任意一点,若![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
(3)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com