
【题目】已知函数f(x)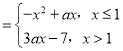 ,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
A.[3,+∞)B.(3,+∞)C.(﹣∞,3)D.(﹣∞,3]
【答案】C
【解析】
当![]() 1,即a<2时,由二次函数的图象和性质,可知存在x1,x2∈(﹣∞,1]且x1≠x2,使得f(x1)=f(x2)成立;当
1,即a<2时,由二次函数的图象和性质,可知存在x1,x2∈(﹣∞,1]且x1≠x2,使得f(x1)=f(x2)成立;当![]() 1,即a≥2时,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则﹣1+a>3a﹣7,由此能求出实数a的取值范围.
1,即a≥2时,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则﹣1+a>3a﹣7,由此能求出实数a的取值范围.
函数f(x)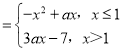 ,
,
存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,
当![]() 1,即a<2时,由二次函数的图象和性质,可知:
1,即a<2时,由二次函数的图象和性质,可知:
存在x1,x2∈(﹣∞,1]且x1≠x2,使得f(x1)=f(x2)成立,
当![]() 1,即a≥2时,
1,即a≥2时,
若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,
则﹣1+a>3a﹣7,
解得a<3,
∴2≤a<3,
综上所述:实数a的取值范围是(﹣∞,3).
故选:C.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和圆
和圆![]() ,倾斜角为45°的直线
,倾斜角为45°的直线![]() 过抛物线
过抛物线![]() 的焦点,且
的焦点,且![]() 与圆
与圆![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)动点![]() 在抛物线
在抛物线![]() 的准线上,动点
的准线上,动点![]() 在
在![]() 上,若
上,若![]() 在
在![]() 点处的切线
点处的切线![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() .求证点
.求证点![]() 在定直线上,并求该定直线的方程.
在定直线上,并求该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)当a=-1时,
①求曲线y= f(x)在点(0,f(0))处的切线方程;
②求函数f(x)的最小值;
(II)求证:当![]() 时,曲线
时,曲线![]() 与
与![]() 有且只有一个交点.
有且只有一个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为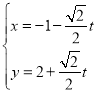 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为![]() ,曲线C2的直角坐标方程为
,曲线C2的直角坐标方程为![]() .
.
(1)若直线l与曲线C1交于M、N两点,求线段MN的长度;
(2)若直线l与x轴,y轴分别交于A、B两点,点P在曲线C2上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,侧面SCD为钝角三角形且垂直于底面ABCD,CD=SD,点M是SA的中点,AD//BC,∠ABC=90°,AB=AD![]() BC=a.
BC=a.

(1)求证:平面MBD⊥平面SCD;
(2)若∠SDC=120°,求三棱锥C﹣MBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自湖北爆发新型冠状病毒肺炎疫情以来,湖北某市医护人员和医疗、生活物资严重匮乏,全国各地纷纷驰援.某运输队接到从武汉送往该市物资的任务,该运输队有8辆载重为6t的A型卡车,6辆载重为10t的B型卡车,10名驾驶员,要求此运输队每天至少运送240t物资.已知每辆卡车每天往返的次数为A型卡车5次,B型卡车4次,每辆卡车每天往返的成本A型卡车1200元,B型卡车1800元,则每天派出运输队所花的成本最低为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD,四边形ABCD是边长为3的正方形,平面![]() 平面
平面![]() ,
,![]() 于点O,
于点O,![]() ,点E在棱PB上,
,点E在棱PB上,![]() .
.
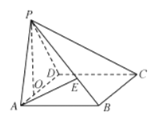
(1)当![]() 时,求直线AE与平面PCD所成角的正弦值;
时,求直线AE与平面PCD所成角的正弦值;
(2)若二面角B-PC-D的余弦值为![]() ,求PO的长.
,求PO的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
②函数![]() 的最小值为2
的最小值为2
③命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
④已知双曲线![]() 过点
过点![]() ,且渐近线为
,且渐近线为![]() ,则离心率
,则离心率![]() ,其中所有正确命题的编号是:_______.
,其中所有正确命题的编号是:_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com