已知全集U=R.集合A=$\left\{{x\left|{\frac{1}{x}＜1}\right.}\right\}$.则∁UA=[0.1]．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

12．已知全集U=R，集合A=$\left\{{x\left|{\frac{1}{x}＜1}\right.}\right\}$，则∁_UA=[0，1]．

分析根据x的正负求出A中不等式的解集确定出A，由全集U=R，求出A的补集即可．

解答解：A中不等式$\frac{1}{x}$＜1，
当x＞0时，解得：x＞1；
当x＜0时，解得：x＜1，此时x＜0，
综上，x的范围为x＜0或x＞1，即A=（-∞，0）∪（1，+∞），
则∁_UA=[0，1]，
故答案为：[0，1]

点评此题考查了补集及其运算，熟练掌握补集的定义是解本题的关键．

练习册系列答案

提分百分百检测卷单元期末测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

2．已知a＞0，函数f（x）=-asin2x-$\sqrt{3}acos2x+b（x∈[0，\frac{π}{2}]）$的值域为[-5，1]，则a，b的值为6$（2-\sqrt{3}）$，12$\sqrt{3}$-23．．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

3．已知集合A={-2，-1，0，1，2}，B={x|-2＜x＜1}，则A∩B=（　　）

A．

{-1，0}

B．

{0，1}

C．

{-1，0，1}

D．

{0，1，2}

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

20．函数f（x）=lg|2x-1|的对称轴为x=$\frac{1}{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

7．已知函数f（x）=x³-x的图象是曲线C
（1）求曲线C在点M（t，f（t））处的切线方程；
（2）求过点P（-1，0）的曲线C的切线方程；
（3）假设a＞0，如果过点（a，b）可以作曲线C的三条切线，证明：-a＜b＜f（a）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

17．已知数列{a_n}满足：a_n+1=f（a_n），n∈N^*．
（1）f（x）=x-sinx，0＜a₁＜1，求证：0＜a_n+1＜a_n＜1；
（2）f（x）=x³-x²+$\frac{x}{2}$+$\frac{1}{4}$，试确定一个首项a₁，使得数列{a_n}为单调数列，并证明你的结论；
（3）f（x）=$\frac{1}{4}$（x²+3），a₁＞0，若对一切n∈N^*，都有a_n+1＞a_n，求a₁的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．

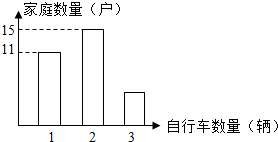某个小区为了制订自行车棚的整修方案，进行了一次以家庭为单位的自行车数量调查．按照家庭成员的人数采用分层抽样的方法，一部分数据如表所示，其中m=2n．通过调查统计了每个家庭的自行车数量，将结果绘制成条形图，如图所示．

家庭人数	1	2	3	4	5
家庭数量	6	m	72		18
抽样数量		4	n	10

（1）计算这个小区的家庭总数和样本容量；
（2）根据图中所显示的统计结果，估计这个小区共有多少辆自行车．
（3）从样本中任取两个家庭，设这两个家庭的自行车数量分别为a和b，记不等式x²-ax+b≤0的解集中整数的个数为η，求η的分布列．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．某集团公司在2013年投入巨资分三期兴建垃圾资源处理厂，1期2013年投入，2期2015年投入，3期2017年投入，具体情况如下表：

1期投入1亿元	建垃圾堆肥厂	造有机肥十多万吨	年收益2千万元
2期投入4亿元	建焚烧发电1厂	年发电1.3亿kw	年收益4千万元
3期投入2亿元	建焚烧发电2厂	年发电1.3亿kw	年收益4千万元

如果每期的投资从第二年开始见效，且不考虑存贷款利息，设2013年以后的n年（2014年第1年）的总收益为f（x）（单位：千万元），试求f（n）的表达式，并预测哪一年能收回全部投资款．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

2．命题“$?x∈（0，\frac{π}{2}）$，sinx＜1”的否定是假命题．（填“真”或“假”）

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学