
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:不详 题型:解答题
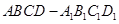 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,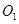 是
是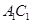 和
和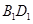 的交点.
的交点.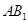 与底面
与底面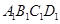 所成的角的大小为
所成的角的大小为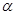 ,二面角
,二面角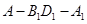 的大小为
的大小为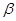 ,试确定
,试确定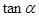 与
与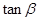 的一个等量关系,并给出证明;
的一个等量关系,并给出证明;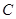 到平面
到平面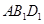 的距离为
的距离为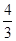 ,求正四棱柱
,求正四棱柱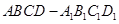 的高.
的高.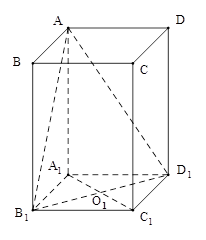
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
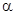 、β和不重合的直线m、n,给出下列命题:
、β和不重合的直线m、n,给出下列命题: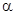 ?m∥
?m∥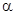 ;
;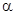 ?m与
?m与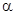 不相交;
不相交;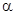 ∩β=m,n∥
∩β=m,n∥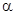 ,n∥β?n∥m;
,n∥β?n∥m;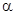 ∥β,m∥β,m
∥β,m∥β,m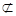
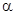 ?m∥
?m∥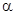 ;
;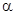 ,n∥β,m∥n?
,n∥β,m∥n?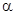 ∥β;
∥β;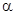 ,n?β,
,n?β,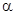 ⊥β?m⊥n;
⊥β?m⊥n;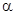 ,n⊥β,
,n⊥β,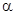 与β相交?m与n相交;
与β相交?m与n相交;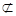 β?m⊥β;
β?m⊥β;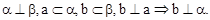
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中, 为底面圆的两条直径,
为底面圆的两条直径, ,且
,且 ⊥
⊥ ,
, ,
,  为
为 的中点.
的中点. ∥平面
∥平面 ;
; 的表面积;
的表面积;  与
与 所成角的正切值.
所成角的正切值. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中, 底面
底面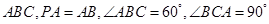 ,
, ,
, 分别在棱
分别在棱 上,且
上,且
 平面
平面 ;
; 为
为 的中点时,求
的中点时,求 与平面
与平面 所成的角的余弦值;
所成的角的余弦值; 使得二面角
使得二面角 为直二面角?并说明理由.
为直二面角?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com